Arbete (fysik)
| Fysikaliskt arbete | |
 | |
| Grundläggande | |
|---|---|
| Definition | Energimängden som omvandlas när en förflyttning sker under inverkan av en kraft |
| Storhetssymbol(er) | |
| Härledningar från andra storheter | W = F · s W = τ θ |
| Enheter | |
| SI-enhet | J = N·m = kg·m2·s−2 |
| SI-dimension | L2·M·T−2 |
| CGS-enhet | erg |
| CGS-dimension | L2·M·T−2 |
Arbete eller fysikaliskt arbete är inom fysiken den energimängd som omvandlas när en förflyttning sker under inverkan av en kraft.
Den härledda SI-enheten för arbete är joule (J) = N·m = W·s = kg·m²/s². Andra enheter är bland andra kilowattimme (kWh), kalori och elektronvolt.
Det arbete som utförs av en konstant kraft med storleken F på en punkt som rör sig en förskjutning s i riktningen för kraften är produkten
Om exempelvis en kraft av 10 newton (F = 10 N) verkar i en punkt som färdas två meter (s = 2 m), utförs ett arbete W = (10 N) (2 m) = 20 Nm = 20 J, vilket ungefär är arbetet att lyfta en 1-kilos vikt från marken till 2 meters höjd mot tyngdkraften. Arbetet fördubblas antingen genom att lyfta dubbla vikten samma avstånd eller genom att lyfta samma vikt dubbla avståndet. Exempel på en lyftanordning:
Om linan dras en sträcka s med kraften F, lyfts lasten sträckan s/2, men kraften som verkar på vikten är 2F, varför det fysikaliska arbetet är detsamma i båda fallen.
Termen arbete introducerades år 1826 av den franske matematikern Gaspard-Gustave Coriolis[1][2] som "vikt lyft till en viss höjd", vilket grundar sig på bruket av tidiga ångmaskiner för att lyfta hinkar med vatten från översvämmade gruvgångar.
Definitioner



Inom mekaniken definieras arbete som skalärprodukten av en kraft- och en avståndsvektor integrerad över en bana enligt
där s1 är banans startpunkt och s2 är banans ändpunkt (se figur 1).
Om kraften F kan beskrivas som gradienten till en potential, till exempel som
där V är en potentialfunktion, sägs F vara en konservativ kraft och det av F uträttade arbetet är oberoende av vägen mellan start- och slutpunkt. Är en potentialfunktion tillgänglig är det möjligt att direkt använda denna enligt
där arbetet är skillnader i potentiell energi. De elektrostatiska och gravitationella fälten är exempel på sådana konservativa fält.
Om kraften inte är konservativ sägs den vara banberoende och har en dissipativ karaktär, det vill säga en större eller mindre del av arbetet är en omvandling till värme. Friktion är ett exempel på det slaget av kraftverkan. En process som innefattar dissipativa krafter är irreversibel.
Om kraften är konstant och konservativ (integralen är oberoende av vägen), kan integralen förenklas enligt
där s är avståndet |s2 - s1| och θ är vinkeln mellan kraften och vägen vald som vektorn s2 - s1. Om kraften och vägen har samma riktning kan integralen förenklas ytterligare till
Arbetet räknas med tecken som beror av kraftens och rörelsens relativa riktningar. Om kraften har en komponent i rörelsens riktning (-90° < θ < 90°) är arbetet positivt och om den har en komponent i motsatt riktning är arbetet negativt. Positivt arbete innebär att energi tillförs det objekt som är föremål för kraftverkan och negativt arbete att objektet förlorar energi. Om kraften och vägens riktningar är vinkelräta mot varandra (cos θ = 0) uträttas inget arbete, vilket till exempel gäller för en rörelse längs en cirkel där kraften är riktad radiellt och vägen är tangentiellt riktad.
Termodynamik
Inom termodynamiken är arbetet en processvariabel. Inom ett termodynamiskt system kan energi distribueras på två sätt, endera i form av värme (till exempel genom upphettning) eller på mekanisk väg (till exempel genom komprimering). Eftersom kompressionskraften verkar längs en väg, är den överförda energin en form av arbete. I båda fallen ändras, i enlighet med termodynamikens första huvudsats, den inre energin hos systemet med (energiprincipen på differentialform, där U (tillståndsfunktion) är systemets inre energi, Q är värmeöverföringen och W arbetet).
Vridmoment och rotation

Ett vridmoment är resultatet av två lika och motsatta krafter (ett kraftpar), som verkar på två olika punkter i en stel kropp. Summan av dessa krafter är noll, men deras effekt på kroppen är vridmomentet T. Vridmomentets arbete beräknas som
där T ⋅ ω är kraften över tiden Δt . Summan av dessa små mängder arbete för hela banan för den stela kroppen ger arbetet
Integralen beräknas längs banan för den stela kroppen med en vinkelhastighet ω som varierar med tiden.
Om vinkelhastighetens vektor bibehåller en konstant riktning, ges den i formen
där φ är vinkeln för vridning kring den konstanta enhetsvektorn S. I detta fall är momentets arbete
där C är banan från φ(t1) till φ(t2). Denna integral beror på rotationsbanan φ(t) och är därför vägberoende.
Om momentvektorn T är parallell med vinkelhastighetsvektorn, så att
och både vridmoment och vinkelhastighet är konstanta, har arbetet formen
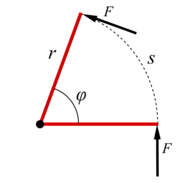
Resultatet kan enklare förstås genom att betrakta det vridmoment som härrör från en kraft av konstant storlek F, vilken anbringas vinkelrätt mot en hävarm på avståndet r, såsom visas i figuren. Denna kraft kommer att verka över avståndet längs cirkelbågen s = rφ, så arbetet är
Introducera vridmoment , för att erhålla
vilket är i enlighet med ovanstående.
Endast den del av vridmomentet som verkar i vinkelhastighetsvektorns riktning bidrar till arbetet.
Exempel
- Kast: en basebollspelare utövar ett positivt arbete på bollen
- Lyft: arbetet som måste utföras på en stationär kropps massa m i ett homogent gravitationsfält med gravitationsaccelerationen g, för att lyfta kroppen sträckan h:
- Rörelse: en massa m ges en hastighet v:
- Töjning: att töja ett elastiskt föremål (som följer Hookes lag, till exempel en fjäder) sträckan s:
- där k är fjäderkonstanten
- Elektricitet: vid förflyttning av den positiva laddningen Q från en punkt till en annan, mellan vilka spänningen är U, måste arbetet
- utföras
- Friktion: i det enklaste fallet och med makroskopiska kroppar, är arbetet produkten av friktionskraften och sträckan. Detta arbete är en omvandling till värme i föremålet och underlaget
Referenser
Noter
- ^ Jammer, Max (1957). Concepts of Force. Dover Publications, Inc. sid. 167; footnote 14. ISBN 0-486-40689-X. https://books.google.com/?id=CZtEBcmOe6gC&printsec=frontcover#PPA167,M1
- ^ Coriolis, Gustave. (1829). Calculation of the Effect of Machines, or Considerations on the Use of Engines and their Evaluation (Du Calcul de l'effet des Machines, ou Considérations sur l'emploi des Moteurs et sur Leur Evaluation). Paris: Carilian-Goeury, Libraire.

























