Ten artykuł dotyczy geometrii. Zobacz też: inne znaczenia terminu wierzchołek.

Wierzchołek – wspólna nazwa kilku pojęć geometrii, zarówno płaskiej, jak i przestrzennej. W każdym przypadku wierzchołek to rodzaj punktu.

• Wierzchołek kąta płaskiego to punkt wspólny jego ramion – dwóch półprostych, które go tworzą^[1].
• Definiuje też się wierzchołek figur geometrycznych, w których można wyróżnić podstawę i najdalej położony od niej punkt, np. w trójkącie^{[potrzebny przypis]}.

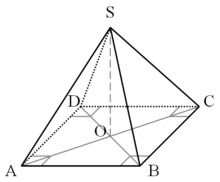
• Wierzchołek bryły to szczególny punkt definiowany dla brył takich jak m.in. stożek czy ostrosłup, który jest najbardziej oddalony od podstawy. Obierając jako podstawę różne ściany, otrzymuje się różne wierzchołki, np. w ostrosłupie. Wierzchołek (S) ułatwia zdefiniowanie wysokości bryły (SO), jako odcinka opuszczonego prostopadle z wierzchołka ku podstawie (ABCD).
• Dla wielościanów wierzchołek może być zdefiniowany niezależnie od podstawy jako wspólny punkt co najmniej trzech ścian.
• Wierzchołek powierzchni stożkowej to definiujący ją punkt, z którego wychodzą tworzące ją proste^[2].

• Wierzchołek linii łamanej to wspólny punkt jej dowolnych dwóch boków – tworzących ją odcinków^[3]. W szczególności: wierzchołek wielokąta to wspólny punkt jego dowolnych dwóch boków^[4].
• Wierzchołek krzywej to punkt, w którym jej promień krzywizny osiąga ekstremum^{[potrzebny przypis]}. Definicja wskazuje na sposób znajdowania wierzchołków. Jeżeli obliczenia okazują się zbyt trudne, można wyznaczyć punkt, w którym krzywizna osiąga ekstremum. Jest to możliwe, ponieważ oba parametry mają ekstrema w tych samych punktach, tylko że w miejscu, gdzie jeden osiąga maksimum – drugi ma minimum. Na przykład:
  • parabola ma jeden wierzchołek (z maksimum krzywizny);
  • elipsa ma 4 wierzchołki (2 z minimum i 2 z maksimum).

• I.N. Bronsztejn, K.A. Siemiendiajew, Matematyka. Poradnik encyklopedyczny, Wydawnictwo Naukowe PWN, Warszawa 1997, wyd. XIV, ISBN 83-01-11658-7