Twierdzenie Bretschneidera

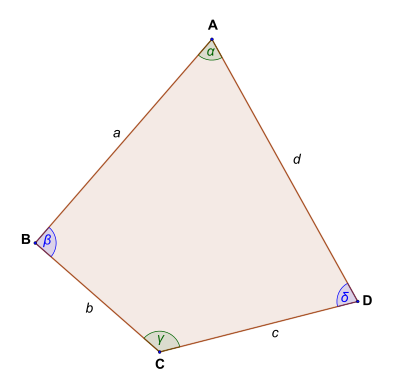
Twierdzenie Bretschneidera – twierdzenie geometryczne pozwalające obliczyć pole powierzchni dowolnego czworokąta znając jedynie długości jego boków oraz miary jego kątów. Zostało ono udowodnione niezależnie w 1842 roku przez Carla Bretschneidera^[1]^[2] oraz przez F. Strehlkego^[2]^[3].

Wypowiedź twierdzenia

Niech dany będzie dowolny czworokąt ABCD o bokach długości

a,

b,

c

i

d,

oraz kątach (kolejno)

\alpha ,

\beta ,

\gamma

i

\delta .

Oznaczmy połowę jego obwodu przez

s={\frac {a+b+c+d}{2}}.

Wtedy pole tego czworokąta wyraża się przez^[4]

S={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}{\frac {\alpha +\gamma }{2}}}}.

Dowód twierdzenia

Przypadek, gdy czworokąt **ABCD** nie jest wypukły.

Na początek zauważmy, że w twierdzeniu nie jest istotne, którą parę przeciwległych kątów – $\alpha$ i $\gamma ,$ czy $\beta$ i $\delta$ – wybierzemy. Zachodzi bowiem

{\begin{aligned}\cos ^{2}{\frac {\beta +\delta }{2}}&=\cos ^{2}{\frac {2\pi -(\alpha +\gamma )}{2}}\\&=\cos ^{2}\left(\pi -{\frac {\alpha +\gamma }{2}}\right)\\&=\left(-\cos {\frac {\alpha +\gamma }{2}}\right)^{2}\\&=\cos ^{2}{\frac {\alpha +\gamma }{2}}.\end{aligned}}

Oznaczmy pole czworokąta symbolem $S.$ Wtedy

{\begin{aligned}S&=S_{\triangle ADB}+S_{\triangle BDC}\\&={\frac {1}{2}}ad\sin \alpha +{\frac {1}{2}}bc\sin \gamma .\end{aligned}}

(1)

Zauważmy, że wzór ten działa zarówno, gdy czworokąt ABCD jest wypukły, jak i gdy jest wklęsły: przypuśćmy, że kąt $\gamma$ ma miarę większą od kąta półpełnego. Wtedy wzór (1) przyjmuje postać

S=S_{\triangle ADB}-S_{\triangle BDC}.

Ale pole trójkąta BDC to

S_{\triangle BDC}={\frac {1}{2}}bc\sin {(2\pi -\gamma )}={\frac {1}{2}}bc\sin(-\gamma )=-{\frac {1}{2}}bc\sin \gamma ,

co ostatecznie daje ponownie wzór (1).

Przemnażając wzór (1) przez 2 i podnosząc obustronnie do kwadratu, otrzymujemy

4S^{2}=(ad)^{2}\sin ^{2}\alpha +(bc)^{2}\sin ^{2}\gamma +2abcd\sin \alpha \sin \gamma .

(2)

Z twierdzenia cosinusów zastosowanego do trójkątów ABD i BCD otrzymujemy

{\begin{aligned}|BD|^{2}&=b^{2}+c^{2}-2bc\cos \gamma \\|BD|^{2}&=a^{2}+d^{2}-2ad\cos \alpha .\end{aligned}}

Łącząc powyższe równości otrzymujemy

a^{2}+d^{2}-b^{2}-c^{2}=2ad\cos \alpha -2bc\cos \gamma .

Podnosząc równość do kwadratu i dzieląc przez 4, otrzymujemy:

{\frac {1}{4}}(a^{2}+d^{2}-b^{2}-c^{2})^{2}=(ad)^{2}\cos ^{2}\alpha +(bc)^{2}\cos ^{2}\gamma -2abcd\cos \alpha \cos \gamma .

(3)

Dodając stronami równania (2) i (3) oraz korzystając z tożsamości trygonometrycznych (jedynki trygonometrycznej, cosinusa sumy kątów oraz cosinusa podwojonego kąta), otrzymujemy kolejno:

{\begin{aligned}4S^{2}+{\frac {1}{4}}(a^{2}+d^{2}-b^{2}-c^{2})^{2}&=(ad)^{2}\cos ^{2}\alpha +(bc)^{2}\cos ^{2}-2abcd\cos \alpha \cos \gamma +(ad)^{2}\sin ^{2}\alpha +(bc)^{2}\sin ^{2}+2abcd\sin \alpha \sin \gamma \\&=(ad)^{2}+(bc)^{2}-2abcd(\cos \alpha \cos \gamma -\sin \alpha \sin \gamma )\\&=(ad)^{2}+(bc)^{2}-2abcd\cos(\alpha +\gamma )\\&=(ad)^{2}+(bc)^{2}-2abcd\cos \left(2\cdot {\frac {\alpha +\gamma }{2}}\right)\\&=(ad)^{2}+(bc)^{2}-2abcd\left(2\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)-1\right)\\&=(ad+bc)^{2}-4abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right).\end{aligned}}

Przemnażając obie strony przez 4 i przenosząc jeden ze składników sumy na drugą stronę, równość przyjmuje postać

16S^{2}=4(ad+bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}-16abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right).

Zapisując wyrażenie

4(ad+bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}

jako

(2ad+2bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}

oraz korzystając z wzorów skróconego mnożenia, otrzymujemy

{\begin{aligned}(2ad+2bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}&=(2ad+2bc+a^{2}+d^{2}-b^{2}-c^{2})(2ad+2bc-a^{2}-d^{2}+b^{2}+c^{2})\\&=((a+d)^{2}-(b-c)^{2})((b+c)^{2}-(a-d)^{2})\\&=(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d).\end{aligned}}

Wprowadzając połowę obwodu $s$

s={\frac {a+b+c+d}{2}},

otrzymujemy równość

16S^{2}=16(s-a)(s-b)(s-c)(s-d)-16abcd\cos ^{2}{\frac {\alpha +\gamma }{2}}

z której, po podzieleniu przez 16 i obustronnym spierwiastkowaniu otrzymujemy wzór Bretschneidera.

Podobne twierdzenia

Twierdzenie Bretschneidera to uogólnienie wzoru Brahmagupty, będącego z kolei uogólnieniem wzoru Herona. Jeśli czworokąt dany jest wpisany w koło, to przeciwległe kąty sumują się do kąta półpełnego i wtedy

S={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}{\frac {\pi }{2}}}}={\sqrt {(s-a)(s-b)(s-c)(s-d)}}.

Bibliografia

Carl Bretschneider. Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes. „C. A. Archiv der Math.”. 2, s. 225–261, 1842.
J.L. Coolidge. A Historically Interesting Formula for the Area of a Quadrilateral.. „Amer. Math. Monthly”. 2, s. 345–347, 1939.
Ernest William Hobson: A treatise on plane geometry. Wyd. IV. Cambridge University Press, 1918.
F. Strehlke. Zwei neue Sätze vom ebenen und shparischen Viereck und Umkehrung des Ptolemaischen Lehrsatzes. „Archiv der Math.”. 2, s. 33–326, 1842.

Linki zewnętrzne

Eric W.E.W. Weisstein Eric W.E.W., Bretschneider’s Formula, [w:] MathWorld, Wolfram Research [dostęp 2020-12-14] (ang.).
Proof Wiki - Bretschneider’s Formula.

[CITEREFBretschneider1842-1] Bretschneider 1842 ↓.

[CITEREFCoolidge1939-2] Coolidge 1939 ↓.

[CITEREFStrehlke1842-3] Strehlke 1842 ↓.

[CITEREFHobson1918204-4] Hobson 1918 ↓, s. 204.

[1]

[2]

[3]

[4]

Fahrer / Team für die Suche eingeben: