Odchylenie standardowe
Odchylenie standardowe – klasyczna miara zmienności, obok średniej arytmetycznej najczęściej stosowane pojęcie statystyczne.
Intuicyjnie rzecz ujmując, odchylenie standardowe mówi, jak szeroko wartości jakiejś wielkości (na przykład wieku, inflacji, kursu walutowego) są rozrzucone wokół jej średniej[a]. Im mniejsza wartość odchylenia tym obserwacje są bardziej skupione wokół średniej.
Odchylenie standardowe jest pierwiastkiem kwadratowym z wariancji[1]. Pojęcie odchylenia zostało wprowadzone przez pioniera statystyki, Karla Pearsona, w 1894 roku[b]. Wyróżnia się:
- odchylenie standardowe zmiennej losowej, będące właściwością badanego zjawiska. Daje się ono obliczyć na podstawie ścisłych informacji o rozkładzie zmiennej losowej[c]. Rozkład ten w praktycznych badaniach nie jest zwykle znany.
- odchylenie standardowe w populacji, które jest liczbą dającą się obliczyć dokładnie, jeśli znane byłyby wartości zmiennej dla wszystkich obiektów populacji; odpowiada odchyleniu zmiennej losowej, której rozkład jest identyczny z rozkładem w populacji.
- odchylenie standardowe z próby, które jest oszacowaniem odchylenia standardowego w populacji na podstawie znajomości wyłącznie części jej obiektów, czyli właśnie próby losowej. Stosowane do tego celu wzory nazywane są estymatorami odchylenia standardowego.
Odchylenie standardowe zmiennej losowej
Odchylenie standardowe zmiennej losowej oznacza się tradycyjnie przez σ (małe greckie sigma) i definiuje jako pierwiastek kwadratowy z wariancji.
Jest ono dane wzorem:
(1) |
gdzie jest wartością oczekiwaną (dowód w przypisie[d]).
Zmienna losowa dyskretna
Dla dyskretnej zmiennej losowej, przyjmującej różnych wartości z prawdopodobieństwami odpowiednio odchylenie standardowe można obliczyć ze wzoru:
gdzie:
Zmienna losowa ciągła
Dla zmiennych ciągłych:
gdzie:
a jest funkcją gęstości prawdopodobieństwa.
Odchylenie standardowe można zdefiniować dla niemal każdego rozkładu prawdopodobieństwa. Istnieją jednak rozkłady (np. rozkład Cauchy’ego), dla których jest ono nieskończone lub nie istnieje.
W przypadku rozkładu normalnego, odchylenie posiada oczywistą interpretację, gdyż jest jednym z parametrów rozkładu, występuje jako we wzorze na gęstość prawdopodobieństwa w tym rozkładzie:
W przypadku innych rozkładów, choć zwykle można podać ścisły wzór wiążący parametry rozkładu z odchyleniem, interpretacja jego wartości jest już znacznie mniej naturalna, o ile w ogóle możliwa.
Dla zmiennych o rozkładach mieszanych dyskretno-ciągłych można zastosować wzór (1).
Odchylenie standardowe w populacji
Dla skończonych populacji odchylenie jest średnią kwadratową z różnic między wartościami zmiennej a ich średnią arytmetyczną. Odchylenie standardowe można obliczyć ze wzoru:
(2) |
gdzie to kolejne wartości cechy w populacji, to wartość oczekiwana, to liczba obserwacji w populacji (dowód drugiej równości w przypisie[e]).
Uwaga: druga równość zachodzi tylko dla skończonej populacji, nie jest prawdziwa w przypadku odchylenia standardowego z próby, gdzie zamiast trzeba wziąć
Dla populacji z mamy więc
Odchylenie standardowe z próby
Odchylenie standardowe w populacji można estymować (przybliżać) odchyleniem standardowym z próby, oznaczanym przez Ponieważ próba niesie informację tylko o części obserwacji z populacji, wynik ten nigdy nie jest dokładny. Wszystkie podane niżej wzory są przybliżeniami, pozwalającymi oszacować odchylenie standardowe zmiennej losowej w populacji (w przypadku rozkładu normalnego jest to również parametr rozkładu σ) na podstawie wartości z próby. Różnice we wzorach biorą się z innych założeń co do pożądanych ich właściwości.
Pierwiastek estymatora nieobciążonego wariancji
Najczęściej używany estymator odchylenia standardowego (błędnie nazywany estymatorem nieobciążonym[f], o czym mowa dalej) ma postać[g]
(3) |
gdzie:
- – kolejne wartości danej zmiennej losowej w próbie,
- – średnia arytmetyczna z próby,
- – średnia arytmetyczna kwadratów wartości z próby,
- – liczba elementów w próbie.
Zaletą tego estymatora jest prostota wzoru, bezpośredni związek z estymatorem nieobciążonym wariancji i relatywnie niewielkie błędy estymacji. Dokładniejszy jest estymator nieobciążony odchylenia (podany dalej), jest jednak trudniejszy w obliczaniu i w związku z tym bardzo rzadko stosowany.
W mianowniku wzoru (3) występuje Wydaje się zupełnie nieintuicyjne, że w przypadku populacji powinno się używać wzoru (2) z w mianowniku, a dla próby wzoru z
Te dwa przypadki różnią się jednak bardzo istotną rzeczą: w przypadku całej populacji znamy dokładną wartość średniej używanej we wzorze (2). W przypadku próby trzeba ją dodatkowo przybliżać średnią z próby Załóżmy, że próba wylosowała się akurat w ten sposób, że w którymś miejscu byłoby drobne zagęszczenie obserwacji w próbce w stosunku do gęstości w całej populacji. Spowoduje to przesunięcie średniej z próby w stronę tego zagęszczenia. Można udowodnić, że suma postaci (czyli taka jak licznik wzorów na odchylenie standardowe) jest najmniejsza gdy więc na skutek tego przesunięcia się średniej w próbce od do odchylenie zmniejsza się. To zmniejszenie licznika jest kompensowane przez mniejszą wartość mianownika ( zamiast ). Szczegółowe wyprowadzenie znajduje się w przypisie[h].
Estymator nieobciążony
Estymator nieobciążony odchylenia standardowego ma tę własność, że gdyby wielokrotnie losować próbę z tej samej populacji i za każdym razem wyliczać odchylenie w próbie i uśredniać otrzymane wartości odchyleń, to wynik dążyłby do prawdziwej wartości odchylenia w populacji.
Statystyka (3) jest często nazywana estymatorem nieobciążonym odchylenia standardowego, jednak nie jest to prawda. To jest estymatorem nieobciążonym wariancji, przy założeniu niezależnego losowania ze zwracaniem elementów próby oraz istnienia skończonej wariancji
Estymator (3) daje w większości przypadków zaniżone wyniki w porównaniu z estymowaną wielkością. Różnica ta jednak dąży do zera wraz ze wzrostem liczebności próby, można więc powiedzieć, że jest asymptotycznie nieobciążony.
Estymator nieobciążony odchylenia standardowego, przy założeniu rozkładu normalnego populacji, dostanie się, dzieląc wartość obliczoną według wzoru (3) przez wielkość:
(4) |
gdzie to funkcja gamma[i]. Wartości szybko zbiegają do 1 wraz ze wzrostem (patrz tabela w Wikiźródłach), korekta jest więc konieczna tylko w przypadku niewielkich prób[j] i potrzeby bardzo dokładnych wyliczeń. Ze względu na trudności obliczeniowe rzadko dokonuje się tej korekty, stosowana jest niemalże jedynie w statystycznej kontroli jakości i w teorii statystyki. W przypadku gdy rozkład nie jest normalny, powyższy estymator może być (i zwykle jest) obciążony. Estymator nieobciążony w niektórych przypadkach nie istnieje.
Współczynnik występuje jeszcze w jednym wzorze – na odchylenie standardowe estymatora odchylenia standardowego podanego powyżej, również przy założeniu rozkładu normalnego populacji:
(5) |
Estymator największej wiarygodności
Estymator największej wiarygodności jest oparty na innym rozumowaniu: Spośród wszystkich rozkładów normalnych postaci czyli posiadających tę samą średnią, co dana próba, ale różne odchylenia, estymator największej wiarygodności podaje taką wartość odchylenia dla której najbardziej prawdopodobne byłoby wylosowanie właśnie takich wyników do próby jakie faktycznie w niej wystąpiły. „Największa wiarygodność” dotyczy zatem nie tyle jego wyników, co raczej próby, która przy takim właśnie odchyleniu w populacji byłaby najbardziej prawdopodobna jako jej losowa reprezentacja. Estymator ten jest jednak obciążony.
(6) |
Estymator największej wiarygodności stosuje się w zasadzie z kilku powodów:
- ze względu na łatwe przedstawienie w postaci średniej i średniej kwadratów
- wzór na estymator największej wiarygodności pokrywa się ze wzorem na odchylenie standardowe w populacji, co pozwala nie przejmować się rozróżnieniem między próbą a populacją,
- najczęstszy, choć niechlubny powód: estymator ten daje najmniejsze wartości odchylenia z wymienionych, przydaje się więc, gdy niewielkie wartości są wskazane dla udowodnienia tezy, którą dane obliczenia mają wspierać.
Istnieje jeszcze jedna popularna metoda wyprowadzania estymatorów – tak zwana metoda momentów. Daje ona w przypadku odchylenia standardowego ten sam wzór (6). Estymator największej wiarygodności jest także asymptotycznie nieobciążony, podobnie jak pierwiastek estymatora nieobciążonego wariancji (3).
Przykład
Przykład pokazuje oszacowanie odchylenia standardowego w populacji za pomocą nieobciążonego estymatora. Próbą będzie wiek czworga dzieci, wyrażony w latach: {5, 6, 8, 9}.
Krok 1. Obliczenie średniej arytmetycznej,
ponieważ są cztery obserwacje:
- Podstawienie 4 zamiast
Krok 2. Obliczenie przybliżenia odchylenia standardowego według wzoru (3):
- Podstawienie 4 pod
- Podstawienie 7 pod
Większość użytkowników odchylenia standardowego kończy w tym miejscu, nie przejmując się obciążeniem estymatora.
Krok 3. Ponieważ próba jest bardzo mała, należy odczytać z tabeli w Wikiźródłach wartość współczynnika dla Wynosi ona 0,9213. Następnie można obliczyć estymator nieobciążony odchylenia standardowego w populacji:
Gdyby nie zastosować korekty w kroku trzecim, wynikiem byłoby 1,8257. Gdyby zastosować estymator największej wiarygodności (6), wynikiem byłoby 1,5811. Dla tak małej próby wskazany jest jednak estymator nieobciążony. Dla dużych prób[j] wszystkie podane estymatory dają wyniki zbliżone do odchylenia w populacji, można więc stosować dowolny z nich. Takie estymatory zwane są asymptotycznie nieobciążonymi.
Podane oszacowanie nie jest tym samym, co odchylenie standardowe w populacji złożonej z takich czterech obiektów. W tym przypadku ze wzoru (2):
Odchylenie standardowe z próby podzielonej na grupy
Wartość estymatora największej wiarygodności można wyliczyć także w przypadku, gdy próba została podzielona na grup i znamy tylko liczności średnie oraz odchylenia standardowe dla wszystkich grup:
gdzie:
- – liczba grup,
- – liczebność -tej grupy,
- – średnia -tej grupy,
- – odchylenie standardowe -tej grupy ze wzoru (6),
- – średnia obserwacji w całej próbie. Można ją wyliczyć za pomocą wzoru na średnią ważoną:
Dla równych liczności grup wzór ten sprowadza się do:
gdzie:
- to średnia z wariancji w poszczególnych grupach,
- to wariancja ze średnich w poszczególnych grupach.
Podobne wzory (nieco bardziej skomplikowane) istnieją także dla estymatora (3).
Szeregi czasowe
Wszystkie powyższe estymatory były wyprowadzane przy założeniu niezależnego losowania ze zwracaniem elementów próby z populacji statystycznej. Warunek ten nie jest spełniony w przypadku, gdy próbą są kolejne wartości jakiegoś czynnika w różnych chwilach czasowych (tzw. szeregi czasowe), np. kursy walut czy akcji. Wówczas bowiem wartości dla zbliżonych chwil czasowych są zwykle skorelowane ze sobą. W takim przypadku wszystkie powyższe wzory są obciążone i nie podają prawdziwej wartości odchylenia w populacji. Nie przeszkadza to graczom giełdowym stosować odchylenia standardowego dla kursów cen akcji w kolejnych dniach (ang. volatility) i opierać na tym wielu metod analizy technicznej, takich jak wstęga Bollingera.
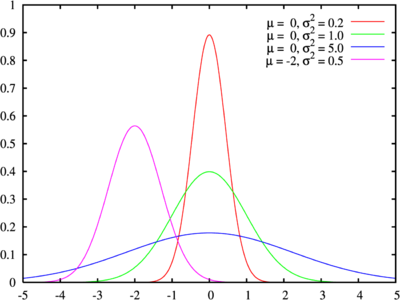
Interpretacja
Im większa wartość odchylenia standardowego tym bardziej obserwowane wielkości oddalone są od średniej. Im mniejsza wartość, tym bardziej są skupione wokół średniej.
Na przykład każda z trzech populacji: ma średnią 7. Ich odchylenia standardowe to odpowiednio 7, 5 i 1. Trzecia populacja ma znacznie mniejsze odchylenie standardowe od pozostałych, gdyż wartości jej elementów są zbliżone do 7.
Odchylenie standardowe może służyć jako miara niepewności. W fizycznym sensie odchylenie standardowe dla grupy powtarzanych pomiarów daje obraz precyzji pomiaru. Kiedy trzeba zdecydować, czy pomiary zgadzają się z teoretycznymi przewidywaniami, ich odchylenie standardowe nabiera kluczowej roli: Jeśli średnia z pomiarów jest zbyt daleko od wartości przewidywanej (przy czym odchylenie standardowe służy tu za jednostkę pomiaru tej odległości), uważa się, że pomiary zaprzeczają przewidywaniom. Oznacza to bowiem, że wypadają one poza zakres wartości, który można by zdroworozsądkowo uznać za prawdopodobny, jeśli przewidywania były słuszne.
Odchylenie a obserwacje dalekie od średniej
Dla rozkładu normalnego

W praktyce często zakłada się, że dane mają rozkład normalny. Założenie to nigdy nie jest całkowicie spełnione. Rozkład normalny ma bowiem niezerową gęstość prawdopodobieństwa dla każdej wartości ze zbioru liczb rzeczywistych, a w realnym świecie wartości zmiennych losowych są zawsze ograniczone, na przykład nie istnieją ludzie o ujemnym wzroście. Bardzo często jednak założenie to jest spełnione z wystarczająco dobrym przybliżeniem. Im lepiej jest ono uzasadnione, tym bliższe prawdy mogą być poniższe stwierdzenia:
- 68% wartości cechy leży w odległości od wartości oczekiwanej,
- 95,5% wartości cechy leży w odległości od wartości oczekiwanej,
- 99,7% wartości cechy leży w odległości od wartości oczekiwanej.
Ostatnie stwierdzenie jest również znane jako reguła trzech sigm.


Wartości dla kilku naturalnych wielokrotności odchylenia przedstawia tabela:
| Maksymalne oddalenie od średniej |
Odsetek obserwacji |
|---|---|
| σ | 0,68268948 |
| 2σ | 0,95449989 |
| 3σ | 0,99730028 |
| 4σ | 0,99993663 |
| 5σ | 0,99999942 |
| 6σ | 0,999999998 |
Poniższa tabela jest często wykorzystywana do wyliczania tzw. przedziału ufności. Np. wiedząc, że zmienna ma rozkład normalny, średnia wynosi 5, a odchylenie 2, można z prawdopodobieństwem 95% przyjąć, że przedział ufności zawiera rzeczywistą wartość parametru (tu: wartości oczekiwanej).
| Odsetek obserwacji | Maksymalne oddalenie od średniej |
|---|---|
| 0,800 | 1,28155σ |
| 0,900 | 1,64485σ |
| 0,950 | 1,95996σ |
| 0,990 | 2,57583σ |
| 0,995 | 2,80703σ |
| 0,999 | 3,29053σ |
Dla dowolnych rozkładów
W ogólnym przypadku, gdy rozkład cech nie jest znany, prawdziwa jest nierówność Czebyszewa: dla danego prawdopodobieństwo, że wartość losowo wybranej cechy różni się od wartości oczekiwanej o więcej niż wynosi co najwyżej Na przykład poza przedziałem leży co najwyżej 25% wartości cechy. Wartości dla kilku naturalnych wielokrotności odchylenia przedstawia tabela:
| Maksymalne oddalenie od średniej |
Odsetek obserwacji |
|---|---|
| 2σ | 0,75 |
| 3σ | 0,8888889 |
| 4σ | 0,9375 |
| 5σ | 0,96 |
Przedziały zawierają mniejszy odsetek obserwacji niż identyczne przedziały dla rozkładu normalnego, ponieważ nierówność Czebyszewa stosuje się dla dowolnego rozkładu, dla którego istnieje odchylenie standardowe.
Jeśli to średnia w populacji, to mediana w populacji, a to odchylenie standardowe w populacji, to spełniona jest też nierówność:
Nie ma przy tym potrzeby dokonywania jakichkolwiek założeń dotyczących rozkładu, włącznie z założeniem o skończoności wariancji[k].
Interpretacja geometryczna
Odchylenie standardowe ma ciekawą interpretację geometryczną. Niech populacja składa się z trzech obserwacji: Niech punkt w przestrzeni trójwymiarowej ma współrzędne Jeśli wówczas odchylenie standardowe w populacji wynosi zero, a punkt znajduje się na osi symetrii układu współrzędnych – prostej Okazuje się, że rzut punktu na prostą odpowiada średniej w populacji – ma współrzędne gdzie a odległość punktu od prostej jest wprost proporcjonalna do odchylenia standardowego:
Ogólnie dla populacji z elementów zachodzi:
jednak całe rozumowanie trzeba przeprowadzać w przestrzeni -wymiarowej.
Własności
Odchylenie standardowe ma szereg własności, które powodują, że jest to miara przydatna w statystyce opisowej.
Skala pomiarowa
Wzory na odchylenie standardowe zawierają różnice wartości obserwowanej i średniej lub wartości oczekiwanej, a więc takie różnice powinny mieć sens dla danej zmiennej. Powinna ona zatem znajdować się na skali interwałowej (przedziałowej) lub absolutnej. W teorii nie powinno się więc stosować odchylenia standardowego do zmiennych ilorazowych (jak np. ceny czy bezrobocie), choć jest to częsta praktyka. Niedopuszczalne jest stosowanie odchylenia do zakodowanych liczbowo zmiennych na skali porządkowej i nominalnej.
Jednostka miary
Odchylenie jest wyrażone w tych samych jednostkach co wartości badanej cechy, np. jeśli mierzony jest wzrost ludzi w cm, to odchylenie standardowe również wyraża się w cm. Jest to niezależne od rozkładu zmiennej.
Zakres
Odchylenie standardowe jest zawsze liczbą nieujemną. Wartość zero ma wtedy i tylko wtedy, gdy wszystkie obserwacje mają tę samą wartość. Odchylenie standardowe w skończonej populacji lub próbce jest zawsze skończone.
Odchylenie sumy i różnicy
Również dla każdego rozkładu odchylenie standardowe sumy lub różnicy dwóch zmiennych losowych jest równe:
-
- gdzie to współczynnik korelacji Pearsona między zmiennymi i
Ogólnie dla zmiennych losowych:
gdzie to kowariancja między zmiennymi i
W szczególności dla dwóch niezależnych zmiennych losowych:
A dla niezależnych zmiennych losowych o tym samym odchyleniu
Działania arytmetyczne zmiennej losowej ze stałą
Jeśli wartości zmiennej losowej o dowolnym rozkładzie zostaną pomnożone lub podzielone przez rzeczywistą stałą odchylenie standardowe odpowiednio pomnoży lub podzieli się przez wartość bezwzględną tej stałej:
Różnica względem wzoru z poprzedniej sekcji wynika stąd, że teraz (dla naturalnego ) zmienna jest dodawana wielokrotnie do niej samej, co odpowiada dodawaniu zmiennych zależnych i skorelowanych na poziomie +1, a poprzednio było dodawane zmiennych niezależnych.
Dodawanie i odejmowanie stałej nie zmienia wartości odchylenia standardowego:
Odchylenie średniej
Z powyższych wzorów na odchylenie sumy niezależnych zmiennych losowych i iloczynu przez stałą wynika praktyczny estymator błędu oszacowania średniej na podstawie próby. Estymator ten zakłada rozkład normalny średniej, jednak przy uśrednianiu dużej[j] liczby obserwacji rozkład średniej zawsze dąży do normalnego (tzw. centralne twierdzenie graniczne), przy dużej[j] liczbie obserwacji można więc stosować ten wzór dla dowolnych rozkładów.
Wzór na średnią w populacji:
Można potraktować realizacje jako zmienne losowe o identycznym rozkładzie Jeśli dodatkowo zmienne te są niezależne (co nie zawsze musi być prawdą, jeśli na przykład jeden pomiar wpływa na następny), wówczas odchylenie średniej:
Ponieważ dla każdego więc:
Szacując za pomocą przybliżenia estymatora nieobciążonego (3), dostaje się przybliżenie nieobciążonego estymatora odchylenia standardowego średniej:
Wrażliwość na błędy obserwacji
Estymatory odchylenia standardowego nie zakładają rozkładu normalnego w populacji. Co prawda „estymator nieobciążony” przy innych rozkładach może posiadać obciążenie, ale nadal można go stosować. W przypadku rozkładu normalnego wyniki mają jednak jasną interpretację, gdyż przekładają się bezpośrednio na prawdopodobieństwo znalezienia obserwacji w określonym oddaleniu od średniej. Dla rozkładów różnych od normalnego prawdopodobieństwo to jest inne, dla bardzo[j] zaburzonych rozkładów z próby odchylenie nic nam o tym prawdpodobieństwie nie powie. W szczególności obecność obserwacji odstających, czyli wartości w próbce bardzo[j] oddalonych od średniej może spowodować powstanie dużych błędów.
Dla najpopularniejszego estymatora (3):
Obliczmy jaki wpływ na błąd końcowego wyniku ma błąd pojedynczej obserwacji W tym celu sprawdzimy, jak zmieni się wartość estymacji kiedy do jednej obserwacji dodamy bardzo małą liczbę Odpowiada to obliczeniu pochodnej cząstkowej po
czyli po skróceniu wpływ błędu pojedynczej obserwacji na błąd estymacji wynosi:
Ze wzoru tego wypływa kilka wniosków:
- Wpływ błędów wprowadzanych przez pojedynczą obserwację na błąd estymacji jest tym większy, im bardziej dana obserwacja jest oddalona od średniej.
- Wpływ błędów pojedynczej obserwacji zmniejsza się, gdy rośnie liczba elementów próby.
- W skrajnych sytuacjach jedna obserwacja odstająca ekstremalnie od średniej może zdominować cały wynik. Przykładowo, gdy wówczas
- i dowolny błąd w obserwacji propaguje się na identyczny błąd w wyniku estymacji.
- Nie należy zatem bezkrytycznie stosować odchylenia standardowego jako miary zmienności dla rozkładów z obserwacjami odstającymi lub bardzo[j] odbiegających od rozkładu normalnego. Wyniki mogą nie mieć wtedy żadnej sensownej interpretacji w praktyce.
Alternatywy dla odchylenia standardowego
Metody rangowe
W przypadku bardzo[j] zaburzonych rozkładów z obserwacjami odstającymi lepiej zastosować metody nieparametryczne. Miary nieparametryczne dają mniej dokładne wyniki w przypadku niezaburzonego rozkładu normalnego, jednak lepsze w przypadku bardzo zaburzonych danych.
Najczęściej jest tutaj stosowany rozstęp ćwiartkowy (rozstęp kwartylny), czyli różnica pomiędzy trzecim i pierwszym kwartylem z próby. Pierwszy kwartyl to liczba, poniżej której znajduje się 25% obserwacji[l]. Trzeci kwartyl to liczba powyżej której jest 25% obserwacji[l]. Pomiędzy nimi znajduje się 50% obserwacji. Połowa rozstępu ćwiartkowego to tzw. odchylenie ćwiartkowe. Miary te są niezależne od rozkładu, dzięki czemu zachowują swoją interpretację w sytuacjach, gdy odchylenie standardowe staje się nieprzydatne.
Ważone odchylenie standardowe
Istnieje też wersja odchylenia standardowego, w której poszczególne obserwacje brane są z różnymi wagami. Odpowiednikiem wzoru (3) jest wówczas:
przy czym wagi muszą być znormalizowane do 1:
Ważone odchylenie standardowe jest najczęściej wykorzystywane do zmniejszenia wrażliwości odchylenia standardowego na obserwacje odstające, co jest osiągane przez nadanie mniejszych wag obserwacjom dalekim od średniej.
Średnie odchylenie bezwzględne
Jeszcze innym podejściem jest obliczanie średniego odchylenia bezwzględnego, czyli wartości:
Miara ta ma tę zaletę, iż błąd każdej obserwacji wchodzi do wyniku z tą samą wagą, jest zatem bardziej odporna na obserwacje odstające.
Odchylenia realne z próby w badaniach społecznych

W badaniach postaw za pomocą Skal Likerta rozkład wyników jest asymetryczny, najczęściej lewostronny. To skutek dążenia wypowiedzi respondentów w kierunku postaw pożądanych, zgodnych z normami uznawanymi za wartości społeczne. Z tego powodu lepszymi miarami rozproszenia są odchylenia realne z próby (Sample Real Deviations), liczone odrębnie dla wyników poniżej przeciętnych i ponadprzeciętnych Odchylenie ujemne obejmuje rezultaty gorsze od średniej, a odchylenie dodatnie rezultaty lepsze od średniej:
gdzie:
- – wagi nadane wypowiedziom pojedynczych respondentów,
- – wartość średnia z wypowiedzi wszystkich respondentów,
- – liczebności podzbiorów oraz w próbie -elementowej.
W obu wzorach występują sumy warunkowe z indeksami selekcyjnymi. Zapis nakazuje sumowanie tylko tych składników które są mniejsze od średniej Analogicznie zapis wytycza składniki o wartości wyższej od [2]
Zobacz też
Uwagi
- ↑ Ściślej: wokół wartości oczekiwanej.
- ↑ Pierwszy raz użyto w: Karl Pearson: Contributions to the Mathematical Theory of Evolution. Philosophical Transactions of the Royal Society of London, 1894. Ser. A, 185, s. 71–110. (praca dostępna tutaj) Na stronie 80 Pearson napisał „Then σ will be termed its standard-deviation (error of mean square)”. Kiedy Ronald Fisher wprowadzał wariancję w 1918, nie wymyślał już nowego symbolu, lecz użył
- ↑ Przy założeniu, że w ogóle odchylenie standardowe dla danego rozkładu istnieje, gdyż zdarzają się (w teorii statystyki) rozkłady, dla których odpowiedni wzór nie jest całkowalny, oraz takie, dla których odchylenie jest nieskończone.
- ↑ Dowód drugiej równości
- ↑ Dowód:
- ↑ Jest nieobciążony asymptotycznie, o czym mowa dalej, jednak „estymator nieobciążony asymptotycznie” i „estymator nieobciążony” to dwa różne pojęcia. Nie każdy estymator nieobciążony asymptotycznie jest estymatorem nieobciążonym i ten akurat nie jest. Istnieją też inne estymatory nieobciążone asymptotycznie odchylenia standardowego.
- ↑ Wyprowadzenie drugiej części wzoru (3):
- ↑ Estymator wariancji z w mianowniku:
- (z definicji)
-
-
- (gdyż ).
- ↑ Wzór na wynika z twierdzenia Cochrana. Zgodnie z nim ma rozkład chi z stopniami swobody.
- ↑ a b c d e f g h W tym artykule, jak w wielu miejscach w statystyce pojawiają się określenia „duża próba”, „rozkład zbliżony do normalnego” itp. Nie są to określenie ścisłe i być nie mogą. Zwykle mówi się w ten sposób, że pewna własność jest spełniona z tym mniejszym błędem im próba jest większa lub rozkład bardziej zbliżony do normalnego. Statystyka jest nauką ścisłą w tym sensie, że przy spełnionych ściśle założeniach istnieje gwarancja używania najdokładniejszych wzorów. Ponieważ jednak założenia nigdy ściśle spełnione nie są, więc właściwy dobór metod jest swego rodzaju sztuką, nie dającą się ściśle sformalizować. Niektórzy ze względów praktycznych zakładają, że „duża próba” ma np. co najmniej 50 obserwacji. Nie ma to jednak żadnych podstaw merytorycznych – ten próg zależy zwykle nie tylko od wielkości próby, ale i od dopuszczalnego błędu i od kształtu rozkładu. Dla jednych prób wystarczy 20 obserwacji, żeby dany wzór można było z sensem stosować, dla innych trzeba 2000.
- ↑ Dowód dwukrotnie wykorzystuje nierówność Jensena:
- ↑ a b W praktyce ta definicja wymaga pewnego uściślenia, zobacz kwantyl.
Przypisy
- ↑ odchylenie standardowe, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2023-03-18].
- ↑ Stanisław Ubermanowicz, Ewaluacja splotowa InfoKultury. Skala dwuważonych ocen, Wydawnictwo Naukowe UAM, Poznań 2005, s. 162–164 ISBN 83-232-1608-8.
Bibliografia
- L. Devroye: A Course in Density Estimation. Birkhäuser, 1987.
- Jacek Koronacki, Jan Mielniczuk: Statystyka dla studentów kierunków technicznych i przyrodniczych. Warszawa: WNT, 2006. ISBN 83-204-3242-1.
- W.J. Krzanowski: Principles of Multivariate Analysis. Nowy Jork: Oxford University Press, 2003, seria: Oxford Statistical Science. ISBN 0-19-850708-9.
- Adam Łomnicki: Wprowadzenie do statystyki dla przyrodników. Wydawnictwo Naukowe PWN, 2005. ISBN 83-01-13979-X.
- Jan Oderfeld, Elżbieta Pleszczyńska: Liniowa estymacja średniego odchylenia w populacji normalnej. Instytut Matematyczny PAN, 1961. Zastosow. Mat. VI, 111–117.
- J. Wawrzynek: Metody opisu i wnioskowania statystycznego. Wrocław: Wydawnictwo Akademii Ekonomicznej im. Oskara Langego we Wrocławiu, 2007, s. 34. ISBN 978-83-7011-859-4.

























































![{\displaystyle s={\sqrt {{\frac {1}{3}}\left[(x_{1}-7)^{2}+(x_{2}-7)^{2}+(x_{3}-7)^{2}+(x_{4}-7)^{2}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8074c97bab40d8d660b945c606e27fe51db5df1)
![{\displaystyle s={\sqrt {{\frac {1}{3}}\left[(5-7)^{2}+(6-7)^{2}+(8-7)^{2}+(9-7)^{2}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d14e3635a95cef91e929d62d6fc821b9ae5a416)









































































![{\displaystyle [l]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4aa3b76a9af835132fd4a1b58954930dd422254)
![{\displaystyle [h].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/765035cd715dc11c890cf271bc0efd8379a60b91)
![{\displaystyle [-d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a4097b5d646aa901ec1a732538c746cdda1ce12)
![{\displaystyle [+d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0535205a8168168cafb9bbe2173293ac0cad2ee8)























![{\displaystyle E(s_{n}^{2})={\frac {1}{n}}E\left[\sum \limits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c257919145e4ba16cba3d6562c1677e1df4d519d)

![{\displaystyle E(s_{n}^{2})={\frac {1}{n}}E\left[\sum \limits _{i=1}^{n}\left((x_{i}-\mu )+(\mu -{\overline {x}})\right)^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1154b8427f6925f0215fd4ffb27e5520fcfe0cd)
![{\displaystyle E(s_{n}^{2})={\frac {1}{n}}\sum \limits _{i=1}^{n}\left[E\left((x_{i}-\mu )^{2}\right)+2E\left((x_{i}-\mu )(\mu -{\overline {x}})\right)+E\left((\mu -{\overline {x}})^{2}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21b026e74eff283e1675e37197bce31275196e64)





![{\displaystyle E(s_{n}^{2})={\frac {1}{n}}\sum \limits _{i=1}^{n}\left[E\left((x_{i}-\mu )^{2}\right)-E\left((\mu -{\overline {x}})^{2}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8dec53068ff51cf825c0f14ae425e55c3800d47)






![{\displaystyle \sigma ^{2}={\frac {n}{n-1}}E(s_{n}^{2})=E\left[{\frac {n}{n-1}}{\frac {1}{n}}\sum \limits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb2e0ebb2948b478f2f0bea933047ad3d1067ef5)
![{\displaystyle \sigma ^{2}=E\left[{\frac {\sum \limits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}{n-1}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b188b00a139f275a3a750f15fa8a5b28e9747294)

