Eisspeedway

Hybrydyzacja (chemia)

Rdzeń atomowy i chmura elektronów w cząsteczce propynu.

Stan elektronów walencyjnych atomu opisują funkcje falowe Ψ, czyli orbitale atomowe (np. s, p), wyznaczane dla elektronów w centralnym polu jądra.

W cząsteczkach związków chemicznych elektrony znajdują się w polu oddziaływania wielu ładunków (rdzeni atomowych i elektronów walencyjnych innych atomów), zajmując orbitale cząsteczkowe. Hipotetyczne orbitale zhybrydyzowane opisują prawdopodobne miejsca znalezienia w cząsteczce elektronów walencyjnych pochodzących od danego atomu

Hybrydyzacja – tworzenie hipotetycznych mieszanych orbitali elektronów atomu w cząsteczce związku chemicznego (rodzaj „orbitali cząsteczkowych”) z pojedynczych „orbitali atomowych” przez liniową kombinację odpowiednich funkcji falowych (zob. przybliżone metody rozwiązywania równania Schrödingera)[a][1]. Wynikiem obliczeń są „funkcje mieszane” opisujące prawdopodobne położenie poszczególnych elektronów walencyjnych w cząsteczce (orbitale zhybrydyzowane, hybrydy). Wyznaczenie hybryd orbitali elektronów walencyjnych pozwala określać możliwości tworzenia wiązań zlokalizowanych i wyznaczać kierunki wiązań sigma w przestrzeni (teoretyczna podstawa stereochemii).

Ukierunkowane wiązania sigma powstają z udziałem elektronów zajmujących takie orbitale zhybrydyzowane, których wzajemne położenie gwarantuje maksymalne nakładanie się orbitali wiążących par elektronowych i najmniejsze wzajemne nakładanie się orbitali antywiążących (minimum energii cząsteczki i największa trwałość). Orbitale wiązań wielokrotnych, np. pi, delta (w tym orbitale sprzężonych wiązań wielokrotnych), powstają w wyniku bocznego nakładania się niezhybrydyzowanych orbitali p lub d, prostopadłych do wiązań sigma[2][3][4][5][6].

Funkcja falowa

Orbital jest definiowany poprzez funkcję falową (Ψ) – rozwiązanie równania Schrödingera np. dla elektronu w polu elektrycznym jądra lub rdzenia atomowego albo wielu jąder atomów, z których jest zbudowana cząsteczka związku chemicznego, i wielu elektronów pochodzących od tych atomów. Klasyczny przykład dotyczy funkcji falowej jednego elektronu w polu centralnym[3][4][5][6].

gdzie:

Orbitale atomowe s, p, d – gęstość elektronowa w polu xy dla różnych liczb kwantowych ℓ i n (m = 0). Zauważalne jest występowanie zwiększonej gęstości w określonych odległościach od jądra. Odległości te w przybliżeniu odpowiadają promieniom orbit w modelu atomu Bohra[3][7]
Orbitale elektronów walencyjnych węgla
(przewiń galerię)
Rdzeń atomowy C (jądro i 1s2) w centrum wykresu xyz
Orbital 2s
Orbitale 2s 2px
Orbitale 2s 2px 2py
Orbitale 2s 2px 2py 2pz
Hybrydy 2sp atomu C*
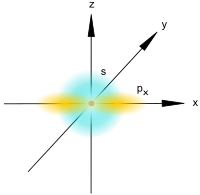
Nie przedstawiono orbitali 2py i 2pz nie ulegających hybrydyzacji.
Hybrydy 2sp2 atomu C*
Nie przedstawiono orbitalu 2pz nie ulegającego tej hybrydyzacji.
Hybrydy 2sp3 atomu C*
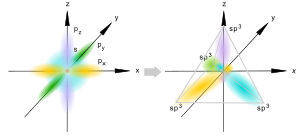
Wszystkie orbitale n = 2 ulegają hybrydyzacji.
– promień orbity w modelu Bohra,
– wielomian Laguerre’a,
– harmonika sferyczna, rozwiązanie równania Laplace’a.

Po wykonaniu obliczeń dla różnych wartości liczb kwantowych:

  • główna: n = 1, 2, 3,...
  • poboczna: l = 0, 1, 2, ..., n-1 (orbitale s, p, d,...)
  • magnetyczna: m = 0, ±1, ±2, ±3,...

i przeliczeniu wartości współrzędnych sferycznych na kartezjańskie otrzymuje się poglądowe graficzne ilustracje orbitali w układzie współrzędnych x, y, z.

Zgodnie z interpretacją Maxa Borna sens fizyczny ma kwadrat modułu funkcji falowej |Ψ|2. Określa on gęstość prawdopodobieństwa napotkania elektronu w punkcie o współrzędnych xyz. Ściany brył ograniczają przestrzeń, w której elektron można napotkać najczęściej (np. prawdopodobieństwo 90%). Linie na konturowych wykresach płaskich są przekrojami tych brył (np. kula dla l = 0, obrotowa „ósemka” dla l = 1).

Przykład atomu węgla

Zasady hybrydyzacji odgrywają największą rolę w chemii organicznej, ze względu na występowanie kilku rodzajów hybryd charakteryzujących elektrony walencyjne atomu węgla. W stanie podstawowym (C): 1s22s22px12py1 (2 niesparowane elektrony walencyjne). W większości związków chemicznych węgiel jest czterowartościowy, co jest związane z występowaniem atomu węgla w stanie wzbudzonym (C*): 1s22s12px12py12pz1(4 niesparowane elektrony walencyjne)[3][7].

  • Atom węgla w stanie podstawowym
  • Atom węgla w stanie wzbudzonym (C*):

Funkcje falowe elektronów walencyjnych węgla, znajdujących się w centralnym polu oddziaływania jądra atomu (funkcje atomowe), nie opisują ich stanu w cząsteczkach związków organicznych, czyli w polu oddziaływania kilku lub wielu różnych jąder i należących do nich elektronów. Za opis stanu w cząsteczce uznaje się zhybrydyzowane (uśrednione, mieszane) funkcje falowe, wyznaczane metodą liniowych kombinacji funkcji atomowych. Zależnie od rodzaju i liczby innych atomów, które stanowią najbliższe cząsteczkowe otoczenie atomu węgla, fizyczny stan jego elektronów walencyjnych opisują funkcje falowe zhybrydyzowanych orbitali[3][7]:

  • sp – kombinacja liniowa Ψl=0 z Ψl=1,
  • sp2 – kombinacja liniowa Ψl=0 z dwiema funkcjami Ψl=1,
  • sp3 – kombinacja liniowa Ψl=0 z trzema funkcjami Ψl=1.

Wynikiem obliczeń są trzy możliwe sposoby opisu zewnętrznej powłoki elektronowej atomu C*:

  • Hybrydyzacja sp:
  • Hybrydyzacja sp2:
  • Hybrydyzacja sp3:

Hybrydyzacja orbitali C* w węglowodorach

Modele cząsteczek alkinów
– efekty hybrydyzacji sp
(przewiń galerię)
Acetylen (HC≡CH)
Propyn (HC≡CCH
3)
1-Butyn (HC≡CCH
2CH
3)
2-Pentyn (CH
3(CH
2)
2C≡CH)
3-Heksyn (HC≡C(CH
2)
3CH
3)
Efekt hybrydyzacji sp w propadienie (CH
2=C=CH
2)

Stan elektronów walencyjnych atomu węgla w cząsteczkach węglowodorów zależy przede wszystkim od liczby jąder węgla i wodoru (protonów) oraz związanych z nimi elektronów w najbliższym „cząsteczkowym otoczeniu” tego atomu. Poszukiwane są funkcje falowe elektronów, które pozwalają utworzyć najbardziej poprawne kwantowe modele cząsteczek różnych węglowodorów, np. alkanów, alkenów i węglowodorów aromatycznych lub allenów. Obliczenia dowodzą, że największą trwałość cząsteczek (najmniejszą wartość energii wewnętrznej) zapewnia hybrydyzacja[3][7]:

sp – w przypadku gdy atom węgla tworzy z atomami sąsiednimi dwa wiązania sigma i dwa wiązania pi (z jednym lub dwoma sąsiadami); minimum wzajemnego nakładania się dwóch hybryd sp jest osiągane, gdy leżą w jednej linii, a więc kąt między wiązaniami sigma w układach −C≡ lub d= jest równy 180° (np. acetylen, alleny)
sp2 – w przypadku, gdy atom węgla tworzy z atomami sąsiednimi trzy wiązania sigma i jedno wiązanie pi; minimum wzajemnego nakładania się trzech hybryd sp2 jest osiągane, gdy są położone na jednej płaszczyźnie i skierowane w stronę wierzchołków opisanego na nich trójkąta równobocznego; a więc kąt między wiązaniami sigma w układach −C= jest równy 120° (np. etylen, benzen, polieny)
sp3 – w przypadku, gdy atom węgla tworzy z atomami sąsiednimi cztery wiązania sigma; minimum wzajemnego nakładania się czterech hybryd sp3 jest osiągane, gdy są skierowane w stronę wierzchołków opisanego na nich tetraedru, a więc kąt między wiązaniami sigma w układach −C− jest równy 109,5° (np. metan, etan i inne alkany)

Przykłady hybrydyzacji w cząsteczkach innych związków

Hybrydyzacja pozwala wyjaśniać struktury takich cząsteczek i jonów, jak dwutlenek węgla (sp), tritlenek siarki (sp2), siarczany (sp3), podtlenek azotu (sp) i inne. Kierunki wiązań określa się uwzględniając wpływ wolnych par elektronowych.

Przykłady hybrydyzacji w cząsteczkach związków nieorganicznych
Efekt hybrydyzacji sp w CO
2
Efekt hybrydyzacji sp2 w SO
3
Efekt hybrydyzacji sp3 w NH
3
Efekt hybrydyzacji sp3 w H
2O
Związek chemiczny Hybrydyzacja
dwutlenek węgla (CO
2) 		sp
tritlenek siarki (SO
3) 		sp2
dwutlenek azotu (NO
2) 		sp2
amoniak (NH
3) 		sp3
woda (H
2O) 		sp3

Inne rodzaje hybrydyzacji

W tabeli zestawiono najważniejsze rodzaje hybrydyzacji, nie ograniczone do wyżej omówionych przypadków hybrydyzacji sp, sp2 i sp3.

Typ cząsteczki Pierwiastki grup głównych/
metale przejściowe 		Tylko metale przejściowe
hybrydyzacja spx hybrydyzacja sdx[8] hybrydyzacja spxdy[9][10]
AX
2
  • linia (180°)
  • hybrydyzacja sp
  • przykład: CO
    2
  • kształt litery V (90°)
  • hybrydyzacja sd
  • przykład: VO+
    2
AX
3
  • płaszczyzna trygonalna (120°)
  • hybrydyzacja sp2
  • przykład: BCl
    3
  • piramida trygonalna (90°)
  • hybrydyzacja sd2
  • przykład: CrO
    3
AX
4
  • tetraedr (109,5°)
  • hybrydyzacja sp3
  • przykład: CCl
    4
  • tetraedr (109,5°)
  • hybrydyzacja sd3
  • przykład: TiCl
    4
  • płaszczyzna kwadratowa (90°)
  • hybrydyzacja sp2d
  • przykład: PtCl2−
    4
AX
6
  • C3v graniastosłup trygonalny (63,4°, 116,6°)
  • hybrydyzacja sd5
  • przykład: W(CH
    3    )
    6
  • oktaedr (90°)
  • hybrydyzacja sp3d2
  • przykład: Mo(CO)
    6
Cząsteczki hiperwartościowościowe[11][12]
(struktury mezomeryczne i uśrednione)
Typ cząsteczki Pierwiastki grup głównych
AX
5 		bipiramida trygonalna (90°, 120°)
AX
6 		oktaedr (90°)
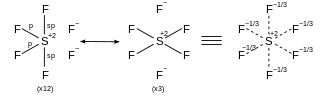
AX7 bipiramida pentagonalna (90°, 72°)

Zobacz też

Uwagi

  1. ↑ Orbitale zhybrydyzowane pomagają wyjaśniać kierunki wiązań chemicznych, ale nie są im przypisywane odpowiednie wartości energii elektronów pochodzących od danego atomu w cząsteczce, w polu oddziaływania rdzeni atomowych i elektronów walencyjnych pozostałych atomów. W tym sensie użyte w definicji pojęcie „orbitali cząsteczkowych” nie odpowiada tak nazywanym orbitalom, otrzymywanym metodą orbitali molekularnych (MO). Hybrydyzacja nie jest więc rzeczywistym fizycznym zjawiskiem powstawania mieszanych (uśrednionych) orbitali elektronów walencyjnych. Według Encyklopedia techniki. Chemia ↓, s. 295 jest „jedynie formalnym zabiegiem matematycznym umożliwiającym wygodny opis wiązań chemicznych i struktury elektronowej cząsteczek”.

Przypisy

  1. ↑ Hybrydyzacja, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2021-07-30].
  2. ↑ Encyklopedia techniki. Chemia, Ewa Czarnecka-Żołek (red.), wyd. 4, Warszawa: Wydawnictwa Naukowo-Techniczne, 1993, ISBN 83-204-1312-5.
  3. ↑ a b c d e f Przykłady zastosowań równania Schrödingera; Widma cząsteczkowe; Fotochemia, [w:] Stanisław Bursa, Chemia fizyczna, Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1979, s. 46–64, 116–154, ISBN 83-01-00152-6.
  4. ↑ a b Janusz Sokołowski, Gotfryd Kupryszewski, Teoretyczne podstawy chemii organicznej, Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1972, s. 46–66, 346–354.
  5. ↑ a b Heinz A. Staab, Wstęp do teoretycznej chemii organicznej, Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1966, s. 75, 124.
  6. ↑ a b N.C. Nenitescu, Chemia organiczna, t. I, Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1967, s. 70–78, 298–310.
  7. ↑ a b c d Antoni Basiński i inni, Chemia fizyczna, wyd. 3, Warszawa: Państwowe Wydawnictwo Naukowe, 1966.
  8. ↑ Frank Weinhold, Clark R. Landis, Valency and bonding: A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge: Cambridge University Press, 2005, s. 381–383, ISBN 0-521-83128-8.
  9. ↑ Craig Bayse, Michael Hall, Prediction of the Geometries of Simple Transition Metal Polyhydride Complexes by Symmetry Analysis, „Journal of the American Chemical Society”, 6, 121, 1999, s. 1348–1358, DOI: 10.1021/ja981965+.
  10. ↑ Gernot Frenking, Nikolaus Fröhlich, The Nature of the Bonding in Transition-Metal Compounds, „Chemical Reviews”, 2, 100, 2000, s. 717–774, DOI: 10.1021/cr980401l.
  11. ↑ David L. Cooper i inni, Chemical Bonding to Hypercoordinate Second-Row Atoms: d Orbital Participation versus Democracy, „Journal of the American Chemical Society”, 10, 116, 1994, s. 4414–4426, DOI: 10.1021/ja00089a033.
  12. ↑ Richard D. Harcourt, Thomas M. Klapötke, Increased valence (qualitative valence bond) descriptions of the electronic structures of electron-rich fluorine-containing molecules, „Journal of Fluorine Chemistry”, 1, 123, 2003, s. 5–20, DOI: 10.1016/S0022-1139(03)00012-5.

Bibliografia

Quelle: https://pl.wikipedia.org/wiki/Hybrydyzacja_(chemia)