User:Tomruen/Convex uniform tetracomb
Regular and uniform honeycombs
There are five fundamental affine Coxeter groups that generate regular and uniform tessellations in 4-space.[1]
| # | Coxeter group | Coxeter-Dynkin diagram | ||
|---|---|---|---|---|
| 1 | A~4 | [(3,3,3,3,3)] | [3[5]] | |
| 2 | B~4 | [4,3,3,4] | ||
| 3 | C~4 | [4,3,31,1] | h[4,3,3,4] | |
| 4 | D~4 | [31,1,1,1] | q[4,3,3,4] | |
| 5 | F~4 | [3,4,3,3] | h[4,3,3,4] | |
There are three regular honeycomb of Euclidean 4-space:
- tesseractic honeycomb, with symbols {4,3,3,4},








 =
= 





 . There are 19 uniform honeycombs in this family.
. There are 19 uniform honeycombs in this family. - 24-cell honeycomb, with symbols {3,4,3,3},








 . There are 31 uniform honeycombs in this family.
. There are 31 uniform honeycombs in this family. - 16-cell honeycomb, with symbols {3,3,4,3},









Other families that generate uniform honeycombs:
- There are 23 uniform honeycombs, 4 unique in the 16-cell honeycomb family. With symbols h{4,32,4} it is geometrically identical to the 16-cell honeycomb,








 =
= 





- There are 7 uniform honeycombs from the A~4,


 family, all unique.
family, all unique. - There are 9 uniform honeycombs in the D~4: [31,1,1,1]




 family, all repeated in other families, including the 16-cell honeycomb.
family, all repeated in other families, including the 16-cell honeycomb.
Non-Wythoffian uniform tessellations in 4-space also exist by elongation (inserting layers), and gyration (rotating layers) from these reflective forms.
The single-ringed tessellations are given below, indexed by Olshevsky's listing.
Duoprismatic forms
- B~2xB~2: [4,4]x[4,4] = [4,3,3,4]










 =
= 







 (Same as tesseractic honeycomb family)
(Same as tesseractic honeycomb family) - B~2xH~2: [4,4]x[6,3]











- H~2xH~2: [6,3]x[6,3]











- A~2xB~2: [Δ]x[4,4]






 (Same forms as [6,3]x[4,4])
(Same forms as [6,3]x[4,4]) - A~2xH~2: [Δ]x[6,3]






 (Same forms as [6,3]x[6,3])
(Same forms as [6,3]x[6,3]) - A~2xA~2: [Δ]x[Δ]


 (Same forms as [6,3]x[6,3])
(Same forms as [6,3]x[6,3])
Prismatic forms
Noncompact prismatic forms
- A3xI~1: [3,3]x[∞] -









- B3xI~1: [4,3]x[∞] -









- H3xI~1: [5,3]x[∞] -









- I~1xI~1xI2r: [∞] x [∞] x [r] = [4,4]x[r] -










 =
= 








Non-Wythoffian forms
The non-Wythoffian forms are built as stacked composites of these prismatic noncompact groups:
- I2pxI~1xA1: [p]x[∞]x[ ] -







 (Prism column)
(Prism column) - D~3xA1: [4,31,1]x[ ]






 (Prism slab)
(Prism slab) - A~3xA1:




 (Prism slab)
(Prism slab) - A~2xI2p: [Δ]x[p]




 (Prism slab)
(Prism slab) - B~2xI2p: [4,4]x[p]







 (Prism slab)
(Prism slab) - H~2xI2p: [6,3]x[p]







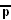
 (Prism slab)
(Prism slab)
B~4 [4,3,3,4] family
| # | Coxeter-Dynkin andSchläfli symbols |
Name | Facets by location: [4,3,3,4] | ||||
|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | |||
[4,3,3] |
[4,3]×[ ] |
[4]×[4] |
[ ]×[3,4] |
[3,3,4] | |||
| 1 | t0{4,3,3,4} |
Tesseractic honeycomb | {4,3,3} |
- | - | - | - |
| 87 | t1{4,3,3,4} |
Rectified tesseractic honeycomb | t1{4,3,3} |
- | - | - | {3,3,4} |
| 88 | t2{4,3,3,4} |
Birectified tesseractic honeycomb (Same as 24-cell honeycomb {3,4,3,3}) |
t1{3,3,4} |
- | - | - | t1{3,3,4} |
| 89 | t0,1{4,3,3,4} |
Truncated tesseractic honeycomb | t0,1{4,3,3} | - | - | - | {3,3,4} |
| 90 | t0,2{4,3,3,4} |
Cantellated tesseractic honeycomb (Small prismatotesseractic honeycomb) |
t0,2{4,3,3} | - | - | {}x{3,4} | t1{3,3,4} |
| 91 | t0,3{4,3,3,4} |
Runcinated tesseractic honeycomb (Small diprismatotesseractic honeycomb) |
|||||
| 92 | t1,2{4,3,3,4} |
Bitruncated tesseractic honeycomb | |||||
| 93 | t1,3{4,3,3,4} |
Bicantellated tesseractic honeycomb (Same as Rectified 24-cell honeycomb t1{3,4,3,3}) |
|||||
| [1] | t0,4{4,3,3,4} |
Stericated tesseractic honeycomb (same as tesseractic honeycomb) |
|||||
| 94 | t0,1,2{4,3,3,4} |
Cantitruncated tesseractic honeycomb (Great prismatotesseractic honeycomb) |
|||||
| 95 | t0,1,3{4,3,3,4} |
Runcitruncated tesseractic honeycomb (Small tomocubic-diprismatotesseractic honeycomb) |
|||||
| 96 | t0,1,4{4,3,3,4} |
Steritruncated tesseractic honeycomb (Tomotesseractic-diprismatotesseractic honeycomb) |
|||||
| 97 | t0,2,3{4,3,3,4} |
Runcicantellated tesseractic honeycomb (Rhombitesseractic-diprismatotesseractic honeycomb) |
|||||
| 98 | t0,2,4{4,3,3,4} |
Stericantellated tesseractic honeycomb (Small rhombitesseractic-prismatotesseractic honeycomb) |
|||||
| 99 | t1,2,3{4,3,3,4} |
Bicantitruncated tesseractic honeycomb (Same as Truncated 24-cell honeycomb, t0,1{3,4,3,3} ) |
|||||
| 100 | t0,1,2,3{4,3,3,4} |
Runcicantitruncated tesseractic honeycomb (Great diprismatotesseractic honeycomb) |
|||||
| 101 | t0,1,2,4{4,3,3,4} |
Stericantitruncated tesseractic honeycomb (Great rhombitesseractic-prismatotesseractic honeycomb) |
|||||
| 102 | t0,1,3,4{4,3,3,4} |
Steriruncitruncated tesseractic honeycomb (Great tomocubic-diprismatotesseractic honeycomb) |
|||||
| 103 | t0,1,2,3,4{4,3,3,4} |
Omnitruncated tesseractic honeycomb | |||||
C~4 [31,1,3,4] family
There are 23 honeycombs in this family,[2] all listed below.
| # | Coxeter-Dynkin andSchläfli symbols File:CDel B5 nodes.png |
Name | Facets by location: [31,1,3,4] | ||||
|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | |||
[3,3,4] |
[31,1,1] |
[3,3]×[ ] |
[ ]×[3]×[ ] |
[3,3,4] | |||
| 104 | {31,1,3,4} |
16-cell honeycomb | {3,3,4} |
{31,1,1} |
- | - | - |
| 105 | t0,1{31,1,3,4} |
Truncated 16-cell honeycomb (Same as truncated 16-cell honeycomb, t0,1{3,3,4,3}) |
|||||
| 106 | t0,2{31,1,3,4} |
Cantellated 16-cell honeycomb (Same as birectified 16-cell honeycomb) |
|||||
| 107 | t0,1,2{31,1,3,4} |
Cantitruncated 16-cell honeycomb (Same as bitruncated 16-cell honeycomb) |
|||||
| 108 | t0,3{31,1,3,4} |
Runcinated 16-cell honeycomb (Small diprismatodemitesseractive honeycomb) |
|||||
| 109 | t0,1,3{31,1,3,4} |
Runcitruncated 16-cell honeycomb (Small prismato16-cell honeycomb) |
|||||
| 110 | t0,2,3{31,1,3,4} |
Runcicantellated 16-cell honeycomb (Great prismato16-cell honeycomb) |
|||||
| 111 | t0,1,2,3{31,1,3,4} |
Runcicantitruncated 16-cell honeycomb (Great diprismato16-cell honeycomb) |
|||||
| [88] | t1{31,1,3,4} |
Rectified 16-cell honeycomb (Same as 24-cell honeycomb, {3,4,3,3}) (Also birectified tesseractic honeycomb) |
t1{3,3,4} |
t1{31,1,1} | - | - | t1{3,3,4} |
| [87] | t2{31,1,3,4} |
Same as rectified tesseractic honeycomb | t1{4,3,3} |
{31,1,1} |
- | - | t1{4,3,3} |
| [1] | t3{31,1,3,4} |
Same as tesseractic honeycomb | {4,3,3} |
- | - | - | {4,3,3} |
| [87] | t0,4{31,1,3,4} |
(Same as Rectified tesseractive honeycomb) | |||||
| [92] | t1,2{31,1,3,4} |
(Same as bitruncated tesseractic honeycomb) | |||||
| [90] | t1,3{31,1,3,4} |
(Same as cantellated tesseractic honeycomb) | |||||
| [89] | t2,3{31,1,3,4} |
(Same as truncated tesseractic honeycomb) | |||||
| [92] | t0,1,4{31,1,3,4} |
(Same as bitruncated tesseractic honeycomb) | |||||
| [93] | t0,2,4{31,1,3,4} |
(Same as rectified 24-cell honeycomb) (Also bicantellated tesseractic honeycomb) |
|||||
| [91] | t0,3,4{31,1,3,4} |
(Same as runcinated tesseractic honeycomb) | |||||
| [94] | t1,2,3{31,1,3,4} |
(Same as cantitruncated tesseractic honeycomb) | |||||
| [99] | t0,1,2,4{31,1,3,4} |
(Same as bicantitruncated tesseractic honeycomb) | |||||
| [97] | t0,1,3,4{31,1,3,4} |
(Same as runcicantellated tesseractic honeycomb) | |||||
| [95] | t0,2,3,4{31,1,3,4} |
(Same as runcitruncated tesseractic honeycomb) | |||||
| [100] | t0,1,2,3,4{31,1,3,4} |
(Same as runcicantitruncated tesseractic honeycomb) | |||||
F~4 [3,4,3,3] family
There are 32 honeycombs in this family, 31 reflective forms and one snub.[3] They are named as truncated forms from the regular 16-cell honeycomb and 24-cell honeycomb. These 31 forms are listed by the regular generators in two groups of 19, with 7 shared between.
From the regular 24-cell honeycomb, 19 forms are:
From the regular 16-cell honeycomb, 19 forms are:
A~4 [3[5]] family
There are 7 honeycombs in this family,[4] all unique to this family, all given below.
| # | Coxeter-Dynkin andSchläfli symbols |
Name | Facets by location | ||||
|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | |||
[3,3,3] |
[ ]x[3,3] |
[3]x[3] |
[3,3]x[ ] |
[3,3,3] | |||
| 134 | {3[5]} |
5-cell honeycomb | |||||
| 135 | t0,1{3[5]} |
Truncated 5-cell honeycomb | |||||
| 136 | t0,2{3[5]} |
Cantellated 5-cell honeycomb | |||||
| 137 | t0,1,2{3[5]} |
Cantitruncated 5-cell honeycomb | |||||
| 138 | t0,1,3{3[5]} |
Runcitruncated 5-cell honeycomb | |||||
| 139 | t0,1,2,3{3[5]} |
Runcicantitruncated 5-cell honeycomb | |||||
| 140 | t0,1,2,3,4{3[5]} |
Omnitruncated 5-cell honeycomb | |||||
D~4 [31,1,1,1] family
There are 9 honeycombs in this family,[5] all repeated, with all 9 forms given below.
| # | Coxeter-Dynkin andSchläfli symbols |
Name | Facets by location: [3,4,3,3] | ||||
|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | |||
| [?] | {31,1,1,1} |
- | |||||
| [104] | t4{31,1,1,1} |
Same as 24-cell honeycomb | - | t1{31,1,1} | t1{31,1,1} | t1{31,1,1} | t1{31,1,1} |
| [?] | t0,4{31,1,1,1} |
- | |||||
| [?] | t0,1{31,1,1,1} |
- | |||||
| [?] | t0,1,4{31,1,1,1} |
- | |||||
| [?] | t0,1,2{31,1,1,1} |
- | |||||
| [?] | t0,1,4{31,1,1,1} |
- | |||||
| [?] | t0,1,2,3{31,1,1,1} |
{}x{}x{}x{} |
t0,2,3{31,1,1} | t0,2,3{31,1,1} | t0,2,3{31,1,1} | t0,2,3{31,1,1} | |
| [?] | t0,1,2,3,4{31,1,1,1} |
{}x{}x{}x{} |
t0,1,2,3{31,1,1} | t0,1,2,3{31,1,1} | t0,1,2,3{31,1,1} | t0,1,2,3{31,1,1} | |
Duoprismatic forms
Coxeter groups:
- B~2xB~2: [4,4]x[4,4]











- B~2xH~2: [4,4]x[6,3]











- H~2xH~2: [6,3]x[6,3]











[4,4]×[4,4]
There are 15 reflective combinatoric forms, but only 3 unique ones.
| # | Coxeter-Dynkin andSchläfli symbols |
Name |
|---|---|---|
| 1 | ||
| [1] | ||
| 6 | ||
| [1] | ||
| [6] | ||
| [1] | ||
| [6] | ||
| [1] | ||
| [6] | ||
| 63 | ||
| [6] | ||
| [63] | ||
| [1] | ||
| [6] | ||
| [63] | ||
| 10 | ||
| [10] | ||
| 67 | ||
| [10] | ||
| [67] |
[4,4]x[6,3]
There are 35 reflective combinatoric forms.
| # | Coxeter-Dynkin | Name |
|---|---|---|
[6,3]x[6,3]
There are 28 reflective combinatoric forms.
| # | Coxeter-Dynkin diagram | Name |
|---|---|---|
References
- ^ George Olshevsky (2006), Uniform Panoploid Tetracombs, manuscript. Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs.
- ^ Olshevsky section V
- ^ Olshevsky section VI
- ^ Olshevsky section VII
- ^ Olshevsky section VII
