Phosphate-buffered saline
Phosphate-buffered saline (PBS) is a buffer solution (pH ~ 7.4) commonly used in biological research. It is a water-based salt solution containing disodium hydrogen phosphate, sodium chloride and, in some formulations, potassium chloride and potassium dihydrogen phosphate. The buffer helps to maintain a constant pH. The osmolarity and ion concentrations of the solutions are isotonic, meaning they match those of the human body.
Applications
PBS has many uses because it is isotonic and non-toxic to most cells. These uses include substance dilution and cell container rinsing. PBS with EDTA is also used to disengage attached and clumped cells. Divalent metals such as zinc, however, cannot be added as this will result in precipitation. For these types of applications, Good's buffers are recommended. PBS has been shown to be an acceptable alternative to viral transport medium regarding transport and storage of RNA viruses, such as SARS-CoV-2.[1]
Preparation
There are many different ways to prepare PBS solutions, common ones are Dulbecco's phosphate-buffered saline (DPBS)[2] and the Cold Spring Harbor protocol.[3] Some formulations of DPBS do not contain potassium and magnesium, while other ones contain calcium and/or magnesium (depending on whether or not the buffer is used on live or fixed tissue: the latter does not require CaCl2 or MgCl2 ).
| Salt | Concentration (mmol/L) | Concentration (g/L) |
|---|---|---|
| Na2HPO4 | 8.1 | 1.15 |
| KH2PO4 | 1.5 | 0.2 |
| NaCl | 137 | 8.0 |
| KCl | 2.7 | 0.2 |
| Salt | Concentration (mmol/L) | Concentration (g/L) |
|---|---|---|
| Na2HPO4 | 8.1 | 1.15 |
| KH2PO4 | 1.5 | 0.2 |
| NaCl | 137 | 8.0 |
| KCl | 2.7 | 0.2 |
| CaCl2 | 0.9 | 0.1 |
| MgCl2 | 0.5 | 0.1 |
| reagent | MW | mass (g) 10× | [mM] 10× | mass (g) 5× | [mM] 5× | mass (g) 1× | [mM] 1× |
|---|---|---|---|---|---|---|---|
| Na2HPO4 | 141.95897 | 14.1960 | 100 | 7.0980 | 50 | 1.41960 | 10 |
| KH2PO4 | 136.08569 | 2.4496 | 18 | 1.2248 | 9 | 0.24496 | 1.8 |
| NaCl | 58.44300 | 80.0669 | 1370 | 40.0335 | 685 | 8.00669 | 137 |
| KCl | 74.55150 | 2.0129 | 27 | 1.0064 | 13.5 | 0.20129 | 2.7 |
| pH = 7.4 |
Start with 800 mL of distilled water to dissolve all salts. Add distilled water to a total volume of 1 liter. The resultant 1× PBS will have a final concentration of 157 mM Na+, 140mM Cl−, 4.45mM K+, 10.1 mM HPO42−, 1.76 mM H2PO4− and a pH of 7.96. Add 2.84 mM of HCl to shift the buffer to 7.3 mM HPO42− and 4.6 mM H2PO4− for a final pH of 7.4 and a Cl− concentration of 142 mM.
The pH of PBS is ~7.4. When making buffer solutions, it is good practice to always measure the pH directly using a pH meter. If necessary, pH can be adjusted using hydrochloric acid or sodium hydroxide.
PBS can also be prepared by using commercially made PBS buffer tablets or pouches.[4]
If used in cell culturing, the solution can be dispensed into aliquots and sterilized by autoclaving or filtration. Sterilization may not be necessary depending on its use. PBS can be stored at room temperature or in the refrigerator. However, concentrated stock solutions may precipitate when cooled and should be kept at room temperature until precipitate has completely dissolved before use.
Dependence of pH on ionic strength and temperature
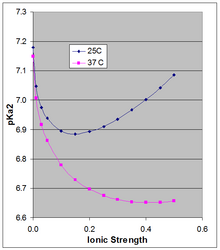
The Henderson–Hasselbalch equation gives the pH of a solution relative to the pKa of the acid–base pair. However the pKa is dependent on ionic strength and temperature, and as it shifts so will the pH of a solution based on that acid–base pair. Because the doubly charged [HPO4]2− is stabilized more by high ionic strength than is the singly-charged [H2PO4]−, their pKa is somewhat dependent on ionic strength. The often-cited pKa of ~7.2 is the value extrapolated to zero ionic strength, and is not applicable at physiological ionic strength.
Phillips et al.[5] measured the pKa at 10, 25, and 37 °C at various ionic strengths. For the latter two temperatures they report pKa in Debye-Hückel equations (plotted in the accompanying figure for μ up to 0.5 M):
at 25 °C: pKa2 = 7.18 − 1.52 sqrt(μ) + 1.96 μ
at 37 °C: pKa2 = 7.15 − 1.56 sqrt(μ) + 1.22 μ
The pKa0 is weakly dependent on temperature. Phillips et al. reported ∆H0 at 25 °C of 760 cal/mol (3180 J/mol) and a linear dependence of pKa0 on 1/T (Van 't Hoff equation). The positive ∆H0 results in an increase in Ka, and thus a decrease in pKa0 with rising temperature, the change in pKa0 being 166 × the change in (1/T), which around 25 °C results in a change in pKa0 of −0.00187 per degree. This applies strictly to the extrapolated thermodynamic pKa0 at infinite dilution, and as the figure shows, the temperature effect can be much larger at higher ionic strength.
See also
References
- ^ Perchetti, G.A.; et al. (2020). "Stability of SARS-CoV-2 RNA in Phosphate-Buffered Saline". Journal of Clinical Microbiology. 58 (8): e01094-20. doi:10.1128/JCM.01094-20. PMC 7383534. PMID 32414839.
- ^ a b c Dulbecco, R.; et al. (1954). "Plaque formation and isolation of pure lines with poliomyelitis viruses". J. Exp. Med. 99 (2): 167–182. doi:10.1084/jem.99.2.167. PMC 2180341. PMID 13130792.
- ^ a b Phosphate-buffered saline (PBS) recipe. CSH Protocol
- ^ Phosphate buffered saline specification sheet. Medicago AB, (2010)
- ^ "Potentiometric Studies of the Secondary Phosphate Ionizations of AMP, ADP, and ATP, and Calculations of Thermodynamic Data for the Hydrolysis Reactions". Biochemistry. 1963. PMID 14069537.
