Laser cooling

Laser cooling includes several techniques where atoms, molecules, and small mechanical systems are cooled with laser light. The directed energy of lasers is often associated with heating materials, e.g. laser cutting, so it can be counterintuitive that laser cooling often results in sample temperatures approaching absolute zero. It is a routine step in many atomic physics experiments where the laser-cooled atoms are then subsequently manipulated and measured, or in technologies, such as atom-based quantum computing architectures. Laser cooling relies on the change in momentum when an object, such as an atom, absorbs and re-emits a photon (a particle of light). For example, if laser light illuminates a warm cloud of atoms from all directions and the laser's frequency is tuned below an atomic resonance, the atoms will be cooled. This common type of laser cooling relies on the Doppler effect where individual atoms will preferentially absorb laser light from the direction opposite to the atom's motion. The absorbed light is re-emitted by the atom in a random direction. After repeated emission and absorption of light the net effect on the cloud of atoms is that they will expand more slowly. The slower expansion reflects a decrease in the velocity distribution of the atoms, which corresponds to a lower temperature and therefore the atoms have been cooled. For an ensemble of particles, their thermodynamic temperature is proportional to the variance in their velocity, therefore the lower the distribution of velocities, the lower temperature of the particles.
The 1997 Nobel Prize in Physics was awarded to Claude Cohen-Tannoudji, Steven Chu, and William Daniel Phillips "for development of methods to cool and trap atoms with laser light".[1]
History
Radiation pressure
Radiation pressure is the force that electromagnetic radiation exerts on matter. In 1873 Maxwell published his treatise on electromagnetism in which he predicted radiation pressure.[2] The force was experimentally demonstrated for the first time by Lebedev and reported at a conference in Paris in 1900,[3] and later published in more detail in 1901.[4] Following Lebedev's measurements Nichols and Hull also demonstrated the force of radiation pressure in 1901,[5] with a refined measurement reported in 1903.[6][7]
Atoms and molecules have bound states and transitions can occur between these states in the presence of light. Sodium is historically notable because it has a strong transition at 589 nm, a wavelength which is close to the peak sensitivity of the human eye. This made it easy to see the interaction of light with sodium atoms. In 1933, Otto Frisch deflected an atomic beam of sodium atoms with light.[8] This was the first realization of radiation pressure acting on an atom or molecule.
Laser cooling proposals
The introduction of lasers in atomic physics experiments was the precursor to the laser cooling proposals in the mid 1970s. Laser cooling was proposed separately in 1975 by two different research groups: Hänsch and Schawlow,[9] and Wineland and Dehmelt.[10] Both proposals outlined the simplest laser cooling process, known as Doppler cooling, where laser light tuned below an atom's resonant frequency is preferentially absorbed by atoms moving towards the laser and after absorption a photon is emitted in a random direction. This process is repeated many times and in a configuration with counterpropagating laser cooling light the velocity distribution of the atoms is reduced.[11]
In 1977 Ashkin submitted a paper which describes how Doppler cooling could be used to provide the necessary damping to load atoms into an optical trap.[12] In this work he emphasized how this could allow for long spectroscopic measurements which would increase precision because the atoms would be held in place. He also discussed overlapping optical traps to study interactions between different atoms.
Initial realizations
Following the laser cooling proposals, in 1978 two research groups that Wineland, Drullinger and Walls of NIST, and Neuhauser, Hohenstatt, Toscheck and Dehmelt of the University of Washington succeeded in laser cooling atoms. The NIST group wanted to reduce the effect of Doppler broadening on spectroscopy. They cooled magnesium ions in a Penning trap to below 40 K. The Washington group cooled barium ions. The research from both groups served to illustrate the mechanical properties of light.[11]
Influenced by the Wineland's work on laser cooling ions, William Phillips applied the same principles to laser cool neutral atoms. In 1982, he published the first paper where neutral atoms were laser cooled.[13] The process used is now known as the Zeeman slower and is a standard technique for slowing an atomic beam.
Modern advances
Atoms

The Doppler cooling limit for electric dipole transitions is typically in the hundreds of microkelvins. In the 1980s this limit was seen as the lowest achievable temperature. It was a surprise then when sodium atoms were cooled to 43 microkelvin when their Doppler cooling limit is 240 microkelvin,[14] this unforeseen low temperature was explained by considering the interaction of polarized laser light with more atomic states and transitions. Previous conceptions of laser cooling were decided to have been too simplistic.[15] The major laser cooling breakthroughs in the 70s and 80s led to several improvements to preexisting technology and new discoveries with temperatures just above absolute zero. The cooling processes were utilized to make atomic clocks more accurate and to improve spectroscopic measurements, and led to the observation of a new state of matter at ultracold temperatures.[16][15] The new state of matter, the Bose–Einstein condensate, was observed in 1995 by Eric Cornell, Carl Wieman, and Wolfgang Ketterle.[17]
Exotic Atoms
Most laser cooling experiments bring the atoms close to at rest in the laboratory frame, but cooling of relativistic atoms has also been achieved, where the effect of cooling manifests as a narrowing of the velocity distribution. In 1990, a group at JGU successfully laser-cooled a beam of 7Li+ at 13.3 MeV in a storage ring [18] from 260 K to lower than 2.9 K, using two counter-propagating lasers addressing the same transition, but at 514.5 nm and 584.8 nm, respectively, to compensate for the large Doppler shift.
Laser cooling of antimatter has also been demonstrated, first in 2021 by the ALPHA collaboration on antihydrogen atoms. [19]
Molecules
Molecules are significantly more challenging to laser cool than atoms because molecules have vibrational and rotational degrees of freedom. These extra degrees of freedom result in more energy levels that can be populated from excited state decays, requiring more lasers compared to atoms to address the more complex level structure. Vibrational decays are particularly challenging because there are no symmetry rules that restrict the vibrational states that can be populated.
In 2010, a team at Yale successfully laser-cooled a diatomic molecule.[20] In 2016, a group at MPQ successfully cooled formaldehyde to 420 μK via optoelectric Sisyphus cooling.[21] In 2022, a group at Harvard successfully laser cooled and trapped CaOH to 720(40) μK in a magneto-optical trap.[22]
Mechanical systems
Starting in the 2000s, laser cooling was applied to small mechanical systems, ranging from small cantilevers to the mirrors used in the LIGO observatory. These devices are connected to a larger substrate, such as a mechanical membrane attached to a frame, or they are held in optical traps, in both cases the mechanical system is a harmonic oscillator. Laser cooling reduces the random vibrations of the mechanical oscillator, removing thermal phonons from the system.
In 2007, an MIT team successfully laser-cooled a macro-scale (1 gram) object to 0.8 K.[23] In 2011, a team from the California Institute of Technology and the University of Vienna became the first to laser-cool a (10 μm × 1 μm) mechanical object to its quantum ground state.[24]
Methods
The first example of laser cooling, and also still the most common method (so much so that it is still often referred to simply as 'laser cooling') is Doppler cooling.
Doppler cooling
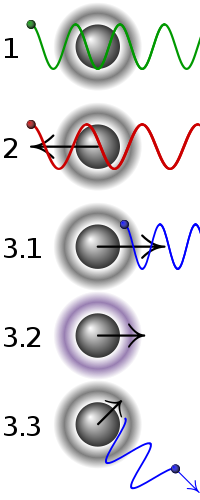
| 1 | A stationary atom sees the laser neither red- nor blue-shifted and does not absorb the photon. |
|---|---|
| 2 | An atom moving away from the laser sees it red-shifted and does not absorb the photon. |
| 31 | An atom moving towards the laser sees it blue-shifted and absorbs the photon, slowing the atom. |
| 32 | The photon excites the atom, moving an electron to a higher quantum state. |
| 33 | The atom re-emits a photon but in a random direction. The atom momentum vectors would add to the original if they were in the same direction but they are not so the atom has lost energy and, therefore, cooled. |
Doppler cooling, which is usually accompanied by a magnetic trapping force to give a magneto-optical trap, is by far the most common method of laser cooling. It is used to cool low density gases down to the Doppler cooling limit, which for rubidium-85 is around 150 microkelvins.
In Doppler cooling, initially, the frequency of light is tuned slightly below an electronic transition in the atom. Because the light is detuned to the "red" (i.e., at lower frequency) of the transition, the atoms will absorb more photons if they move towards the light source, due to the Doppler effect. Thus if one applies light from two opposite directions, the atoms will always scatter more photons from the laser beam pointing opposite to their direction of motion. In each scattering event the atom loses a momentum equal to the momentum of the photon. If the atom, which is now in the excited state, then emits a photon spontaneously, it will be kicked by the same amount of momentum, but in a random direction. Since the initial momentum change is a pure loss (opposing the direction of motion), while the subsequent change is random, the probable result of the absorption and emission process is to reduce the momentum of the atom, and therefore its speed—provided its initial speed was larger than the recoil speed from scattering a single photon. If the absorption and emission are repeated many times, the average speed, and therefore the kinetic energy of the atom, will be reduced. Since the temperature of a group of atoms is a measure of the average random internal kinetic energy, this is equivalent to cooling the atoms.
Other methods
Other methods of laser cooling include:
- Sisyphus cooling[25]
- Resolved sideband cooling
- Raman sideband cooling
- Velocity selective coherent population trapping (VSCPT)[26]
- Gray molasses
- Optical molasses
- Cavity-mediated cooling[27]
- Use of a Zeeman slower
- Electromagnetically induced transparency (EIT) cooling[28]
- Anti-Stokes cooling in solids
- Polarization gradient cooling
Applications
Laser cooling is very common in the field of atomic physics. Reducing the random motion of atoms has several benefits, including the ability to trap atoms with optical or magnetic fields. Spectroscopic measurements of a cold atomic sample will also have reduced systematic uncertainties due to thermal motion.
Often multiple laser cooling techniques are used in a single experiment to prepare a cold sample of atoms, which is then subsequently manipulated and measured. In a representative experiment a vapor of strontium atoms is generated in a hot oven that exit the oven as an atomic beam. After leaving the oven the atoms are Doppler cooled in two dimensions transverse to their motion to reduce loss of atoms due to divergence of the atomic beam. The atomic beam is then slowed and cooled with a Zeeman slower to optimize the atom loading efficiency into a magneto-optical trap (MOT), which Doppler cools the atoms, that operates on the 1S0 → 1P1 with lasers at 461 nm. The MOT transitions from using light at 461 nm to using light at 689 nm to drive the 1S0 → 3P1, which is a narrow transition, to realize even colder atoms. The atoms are then transferred into an optical dipole trap where evaporative cooling gets them to temperatures where they can be effectively loaded into an optical lattice.
Laser cooling is important for quantum computing efforts based on neutral atoms and trapped atomic ions. In an ion trap Doppler cooling reduces the random motion of the ions so they form a well-ordered crystal structure in the trap. After Doppler cooling the ions are often cooled to their motional ground state to reduce decoherence during quantum gates between ions.
Equipment
Laser cooling atoms (and molecules especially) requires specialized experimental equipment that when assembled forms a cold atom machine. Such a machine generally consists of two parts: a vacuum chamber which houses the laser cooled atoms and the laser systems used for cooling, as well as for preparing and manipulating atomic states and detecting the atoms.
Vacuum system
In order for atoms to be laser cooled, the atoms cannot collide with room temperature background gas particles. Such collisions will drastically heat the atoms, and knock them out of weak traps. Acceptable collision rates for cold atom machines typically require vacuum pressures at 10−9 Torr, and very often hundreds or even thousands of times lower pressures are necessary. To achieve these low pressures, a vacuum chamber is needed. The vacuum chamber typically includes windows so that the atoms can be addressed with lasers (e.g. for laser cooling) and light emitted by the atoms or absorption of light be the atoms can be detected. The vacuum chamber also requires an atomic source for the atom(s) to be laser cooled. The atomic source is generally heated to produce thermal atoms that can be laser cooled. For ion trapping experiments the vacuum system must also hold the ion trap, with the appropriate electric feedthroughs for the trap. Neutral atom systems very often employ a Magneto-optical trap (MOT) as one of the early stages in collecting and cooling atoms. For a MOT typically magnetic field coils are placed outside of the vacuum chamber to generate magnetic field gradients for the MOT.
Lasers
The lasers required for cold atom machines are entirely dependent on the choice of atom. Each atom has unique electronic transitions at very distinct wavelengths that must be driven for the atom to be laser cooled. Rubidium, for example is a very commonly used atom which requires driving two transitions with laser light at 780 nm that are separated by a few GHz. The light for rubidium can be generated from a signal laser at 780 nm and an Electro-optic modulator. Generally tens of mW (and often hundreds of mW to cool significantly more atoms) is used to cool neutral atoms. Trapped ions on the other hand require microwatts of optical power, as they are generally tightly confined and the laser light can be focused to a small spot size. The strontium ion, for example requires light at both 422 nm and 1092 nm in order to be Doppler cooled. Because of the small Doppler shifts involved with laser cooling, very narrow lasers, order of a few MHz, are required for laser cooling. Such lasers are generally stabilized to spectroscopy reference cells, optical cavities, or sometimes wavemeters so the laser light can be precisely tuned relative to the atomic transitions.
See also
- List of laser articles
- Optical tweezers – Scientific instruments
- Zeeman Slower – Instrument for slowing and cooling a beam of hot atoms
- Mössbauer effect – Resonant and recoil-free emission and absorption of gamma radiation by atomic nuclei
- Mössbauer spectroscopy – Spectroscopic technique
- Quantum refrigerators
- Timeline of low-temperature technology
- Particle beam cooling
References
- ^ "The Nobel Prize in Physics 1997". Nobel Foundation. Archived from the original on 7 October 2008. Retrieved 9 October 2008.
- ^
Maxwell, J.C. (1873). A Treatise on Electricity and Magnetism, II (1st ed.). Oxford. p. 391.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Lebedew, Pyotr (1900). Les forces de Maxwell-Bartoli dues à la pression de la lumière (PDF). Rapports présentés au Congrès International de Physique (in French). Vol. 2. Paris. p. 133.
- ^ Lebedew, P. (1901). "Untersuchungen über die Druckkräfte des Lichtes". Annalen der Physik (in German). 311 (11): 433–458. Bibcode:1901AnP...311..433L. doi:10.1002/andp.19013111102.
- ^ Nichols, E.F.; Hull, G.F. (1901). "A Preliminary Communication on the Pressure of Heat and Light Radiation". Physical Review. Series I. 13 (5): 307–320. Bibcode:1901PhRvI..13..307N. doi:10.1103/PhysRevSeriesI.13.307.
- ^ Nichols, E.F.; Hull, G.F. (1903). "The Pressure Due To Radiation . (Second Paper.)". Physical Review. 17 (1): 26–50. Bibcode:1903PhRvI..17...26N. doi:10.1103/PhysRevSeriesI.17.26.
- ^ Nichols, E.F.; Hull, G.F. (1903). "The Pressure Due To Radiation. (Second Paper.)". Physical Review. 17 (2): 91–104. Bibcode:1903PhRvI..17...91N. doi:10.1103/PhysRevSeriesI.17.91.
- ^ Frisch, R. (1933). "Experimenteller Nachweis des Einsteinschen Strahlungsrückstoßes". Zeitschrift für Physik (in German). 86 (1–2): 42–48. Bibcode:1933ZPhy...86...42F. doi:10.1007/BF01340182. S2CID 123038196.
- ^ Hänsch, T. W.; Schawlow, A. L. (January 1975). "Cooling of gases by laser radiation". Optics Communications. 13 (1): 68–69. Bibcode:1975OptCo..13...68H. doi:10.1016/0030-4018(75)90159-5.
- ^ Wineland, David; Dehmelt, Hans (January 1, 1975). "Proposed 1014 ∆ν < ν laser fluorescence spectroscopy on T1+ mono-ion oscillator III". Bulletin of the American Physical Society. 20 (4): 637.
- ^ a b Phillips, William D. (1998). "Nobel Lecture: Laser cooling and trapping of neutral atoms". Reviews of Modern Physics. 70 (3): 721–741. Bibcode:1998RvMP...70..721P. doi:10.1103/revmodphys.70.721.
- ^ Ashkin, A. (20 March 1978). "Trapping of Atoms by Resonance Radiation Pressure". Physical Review Letters. 40 (12): 729–732. Bibcode:1978PhRvL..40..729A. doi:10.1103/PhysRevLett.40.729.
- ^ Phillips, William (1 March 1982). "Laser Deceleration of an Atomic Beam". Physical Review Letters. 48 (9): 596–599. Bibcode:1982PhRvL..48..596P. doi:10.1103/PhysRevLett.48.596.
- ^ Paul D. Lett; Richard N. Watts; Christoph I. Westbrook; William D. Phillips; A. Winnicki; Phillip L. Gould; Harold J. Metcalf (1988). "Observation of Atoms Laser Cooled below the Doppler Limit". Physical Review Letters. 61 (2): 169–172. Bibcode:1988PhRvL..61..169L. doi:10.1103/PhysRevLett.61.169. PMID 10039050. S2CID 8479501.
- ^ a b Bardi, Jason Socrates (2008-04-02). "Focus: Landmarks: Laser Cooling of Atoms". Physics. 21: 11. doi:10.1103/physrevfocus.21.11.
- ^ Adams, Charles S.; Riis, Erling. "Laser Cooling and Manipulation of Neutral Particles" (PDF). New Optics. Archived from the original (PDF) on 2017-11-15. Retrieved 2017-05-06.
- ^ Chin, Cheng (1 June 2016). "Ultracold atomic gases going strong". National Science Review. 3 (2): 168–170. doi:10.1093/nsr/nwv073.
- ^ Schröder, S.; Klein, R.; Boos, N.; Gerhard, M.; Grieser, R.; Huber, G.; Karafillidis, A.; Krieg, M.; Schmidt, N.; Kühl, T.; Neumann, R.; Balykin, V.; Grieser, M.; Habs, D.; Jaeschke, E.; Krämer, D.; Kristensen, M.; Music, M.; Petrich, W.; Schwalm, D.; Sigray, P.; Steck, M.; Wanner, B.; Wolf, A. (11 June 1990). "First laser cooling of relativistic ions in a storage ring". Physical Review Letters. 64 (24): 2901–2904. Bibcode:1990PhRvL..64.2901S. doi:10.1103/PhysRevLett.64.2901. PMID 10041842.
- ^ Baker, C. J.; Bertsche, W.; Capra, A.; Carruth, C.; Cesar, C. L.; Charlton, M.; Christensen, A.; Collister, R.; Mathad, A. Cridland; Eriksson, S.; Evans, A.; Evetts, N.; Fajans, J.; Friesen, T.; Fujiwara, M. C.; Gill, D. R.; Grandemange, P.; Granum, P.; Hangst, J. S.; Hardy, W. N.; Hayden, M. E.; Hodgkinson, D.; Hunter, E.; Isaac, C. A.; Johnson, M. A.; Jones, J. M.; Jones, S. A.; Jonsell, S.; Khramov, A.; Knapp, P.; Kurchaninov, L.; Madsen, N.; Maxwell, D.; McKenna, J. T. K.; Menary, S.; Michan, J. M.; Momose, T.; Mullan, P. S.; Munich, J. J.; Olchanski, K.; Olin, A.; Peszka, J.; Powell, A.; Pusa, P.; Rasmussen, C. Ø; Robicheaux, F.; Sacramento, R. L.; Sameed, M.; Sarid, E.; Silveira, D. M.; Starko, D. M.; So, C.; Stutter, G.; Tharp, T. D.; Thibeault, A.; Thompson, R. I.; van der Werf, D. P.; Wurtele, J. S. (April 2021). "Laser cooling of antihydrogen atoms". Nature. 592 (7852): 35–42. Bibcode:2021Natur.592...35B. doi:10.1038/s41586-021-03289-6. PMC 8012212. PMID 33790445.
- ^ E. S. Shuman; J. F. Barry; D. DeMille (2010). "Laser cooling of a diatomic molecule". Nature. 467 (7317): 820–823. arXiv:1103.6004. Bibcode:2010Natur.467..820S. doi:10.1038/nature09443. PMID 20852614. S2CID 4430586.
- ^ Prehn, Alexander; Ibrügger, Martin; Glöckner, Rosa; Rempe, Gerhard; Zeppenfeld, Martin (10 February 2016). "Optoelectrical Cooling of Polar Molecules to Submillikelvin Temperatures". Physical Review Letters. 116 (6): 063005. arXiv:1511.09427. Bibcode:2016PhRvL.116f3005P. doi:10.1103/PhysRevLett.116.063005. PMID 26918988. Retrieved 10 January 2024.
- ^ N. B. Vilas; C. Hallas; L. Anderegg; P. Robichaud; A. Winnicki; D. Mitra; J. M. Doyle (2022). "Magneto-optical trapping and sub-Doppler cooling of a polyatomic molecule". Nature. 606 (7912): 70–74. arXiv:2112.08349v1. Bibcode:2022Natur.606...70V. doi:10.1038/s41586-022-04620-5. PMID 35650357. S2CID 245144894.
- ^ "Laser-cooling Brings Large Object Near Absolute Zero". ScienceDaily.
- ^ "Caltech Team Uses Laser Light to Cool Object to Quantum Ground State". Caltech.edu. 5 October 2011. Retrieved June 27, 2013.
- ^ Laser cooling and trapping of neutral atoms Nobel Lecture by William D. Phillips, Dec 8, 1997: Phillips, William D. (1998). "Nobel Lecture: Laser cooling and trapping of neutral atoms". Reviews of Modern Physics. 70 (3): 721–741. Bibcode:1998RvMP...70..721P. doi:10.1103/RevModPhys.70.721.
- ^ A. Aspect; E. Arimondo; R. Kaiser; N. Vansteenkiste; C. Cohen-Tannoudji (1988). "Laser Cooling below the One-Photon Recoil Energy by Velocity-Selective Coherent Population Trapping". Physical Review Letters. 61 (7): 826–829. Bibcode:1988PhRvL..61..826A. doi:10.1103/PhysRevLett.61.826. PMID 10039440.
- ^ Peter Horak; Gerald Hechenblaikner; Klaus M. Gheri; Herwig Stecher; Helmut Ritsch (1988). "Cavity-Induced Atom Cooling in the Strong Coupling Regime". Physical Review Letters. 79 (25): 4974–4977. Bibcode:1997PhRvL..79.4974H. doi:10.1103/PhysRevLett.79.4974.
- ^ Haller, Elmar; Hudson, James; Kelly, Andrew; Cotta, Dylan A.; Peaudecerf, Bruno; Bruce, Graham D.; Kuhr, Stefan (2015). "Single-atom imaging of fermions in a quantum-gas microscope". Nature Physics. 11 (9): 738–742. arXiv:1503.02005. Bibcode:2015NatPh..11..738H. doi:10.1038/nphys3403. S2CID 51991496.
Additional sources
- Foot, C. J. (2005). Atomic Physics. Oxford University Press. ISBN 978-0-19-850695-9.
- Cohen-Tannoudji, Claude; Guéry-Odelin, David (2011). Advances in Atomic Physics. doi:10.1142/6631. ISBN 978-981-277-496-5.
- Bowley, Roger; Copeland, Ed (2010). "Laser Cooling". Sixty Symbols. Brady Haran for the University of Nottingham.
- Laser Cooling HyperPhysics
- PhysicsWorld series of articles by Chad Orzel:
- Cold: how physicists learned to manipulate and move particles with laser cooling
- Colder: how physicists beat the theoretical limit for laser cooling and laid the foundations for a quantum revolution
- Coldest: how a letter to Einstein and advances in laser-cooling technology led physicists to new quantum states of matter
