In quantum chemistry, a conical intersection of two or more potential energy surfaces is the set of molecular geometry points where the potential energy surfaces are degenerate (intersect) and the non-adiabatic couplings between these states are non-vanishing. In the vicinity of conical intersections, the Born–Oppenheimer approximation breaks down and the coupling between electronic and nuclear motion becomes important, allowing non-adiabatic processes to take place. The location and characterization of conical intersections are therefore essential to the understanding of a wide range of important phenomena governed by non-adiabatic events, such as photoisomerization, photosynthesis, vision and the photostability of DNA.

Conical intersections are also called molecular funnels or diabolic points as they have become an established paradigm for understanding reaction mechanisms in photochemistry as important as transitions states in thermal chemistry. This comes from the very important role they play in non-radiative de-excitation transitions from excited electronic states to the ground electronic state of molecules.^[1] For example, the stability of DNA with respect to the UV irradiation is due to such conical intersection.^[2] The molecular wave packet excited to some electronic excited state by the UV photon follows the slope of the potential energy surface and reaches the conical intersection from above. At this point the very large vibronic coupling induces a non-radiative transition (surface-hopping) which leads the molecule back to its electronic ground state. The singularity of vibronic coupling at conical intersections is responsible for the existence of Geometric phase, which was discovered by Longuet-Higgins^[3] in this context.

Degenerate points between potential energy surfaces lie in what is called the intersection or seam space with a dimensionality of 3N-8 (where N is the number of atoms). Any critical points in this space of degeneracy are characterised as minima, transition states or higher-order saddle points and can be connected to each other through the analogue of an intrinsic reaction coordinate in the seam. In benzene, for example, there is a recurrent connectivity pattern where permutationally isomeric seam segments are connected by intersections of a higher symmetry point group.^[4] The remaining two dimensions that lift the energetic degeneracy of the system are known as the branching space.

In order to be able to observe it, the process would need to be slowed down from femtoseconds to milliseconds. A novel 2023 quantum experiment, involving trapped-ion quantum computer, slowed down interference pattern of a single atom (caused by a conical intersection) by a factor of 100 billion, making a direct observation possible.^[5]

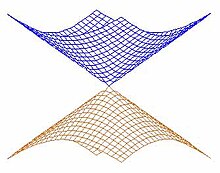
Conical intersections are ubiquitous in both trivial and non-trivial chemical systems. In an ideal system of two dimensionalities, this can occur at one molecular geometry. If the potential energy surfaces are plotted as functions of the two coordinates, they form a cone centered at the degeneracy point. This is shown in the adjacent picture, where the upper and lower potential energy surfaces are plotted in different colors. The name conical intersection comes from this observation.

In diatomic molecules, the number of vibrational degrees of freedom is 1. Without the necessary two dimensions required to form the cone shape, conical intersections cannot exist in these molecules. Instead, the potential energy curves experience avoided crossings if they have the same point group symmetry, otherwise they can cross.

In molecules with three or more atoms, the number of degrees of freedom for molecular vibrations is at least 3. In these systems, when spin–orbit interaction is ignored, the degeneracy of conical intersection is lifted through first order by displacements in a two dimensional subspace of the nuclear coordinate space.

The two-dimensional degeneracy lifting subspace is referred to as the branching space or branching plane. This space is spanned by two vectors, the difference of energy gradient vectors of the two intersecting electronic states (the g vector), and the non-adiabatic coupling vector between these two states (the h vector). Because the electronic states are degenerate, the wave functions of the two electronic states are subject to an arbitrary rotation. Therefore, the g and h vectors are also subject to a related arbitrary rotation, despite the fact that the space spanned by the two vectors is invariant. To enable a consistent representation of the branching space, the set of wave functions that makes the g and h vectors orthogonal is usually chosen. This choice is unique up to the signs and switchings of the two vectors, and allows these two vectors to have proper symmetry when the molecular geometry is symmetric.

The degeneracy is preserved through first order by differential displacements that are perpendicular to the branching space. The space of non-degeneracy-lifting displacements, which is the orthogonal complement of the branching space, is termed the seam space. Movement within the seam space will take the molecule from one point of conical intersection to an adjacent point of conical intersection. The degeneracy space connecting different conical intersections can be explored and characterised using band and molecular dynamics methods.^[6]

For an open shell molecule, when spin-orbit interaction is added to the,^{[clarification needed]} the dimensionality of seam space is reduced.^[7]

The presence of conical intersections can be detected experimentally.^[8] It has been proposed that two-dimensional spectroscopy can be used to detect their presence through the modulation of the frequency of the vibrational coupling mode.^[9] A more direct spectroscopy of conical intersections, based on ultrafast X-ray transient absorption spectroscopy, was proposed, offering new approaches to their study.^[10]

Conical intersections can occur between electronic states with the same or different point group symmetry, with the same or different spin symmetry. When restricted to a non-relativistic Coulomb Hamiltonian, conical intersections can be classified as symmetry-required, accidental symmetry-allowed, or accidental same-symmetry, according to the symmetry of the intersecting states.

A symmetry-required conical intersection is an intersection between two electronic states carrying the same multidimensional irreducible representation. For example, intersections between a pair of E states at a geometry that has a non-abelian group symmetry (e.g. C_3h, C_3v or D_3h). It is named symmetry-required because these electronic states will always be degenerate as long as the symmetry is present. Symmetry-required intersections are often associated with Jahn–Teller effect.

An accidental symmetry-allowed conical intersection is an intersection between two electronic states that carry different point group symmetry. It is called accidental because the states may or may not be degenerate when the symmetry is present. Movement along one of the dimensions along which the degeneracy is lifted, the direction of the difference of the energy gradients of the two electronic states, will preserve the symmetry while displacements along the other degeneracy lifting dimension, the direction of the non-adiabatic couplings, will break the symmetry of the molecule. Thus, by enforcing the symmetry of the molecule, the degeneracy lifting effect caused by inter-state couplings is prevented. Therefore, the search for a symmetry-allowed intersection becomes a one-dimensional problem and does not require knowledge of the non-adiabatic couplings, significantly simplifying the effort. As a result, all the conical intersections found through quantum mechanical calculations during the early years of quantum chemistry were symmetry-allowed intersections.

An accidental same-symmetry conical intersection is an intersection between two electronic states that carry the same point group symmetry. While this type of intersection was traditionally more difficult to locate, a number of efficient searching algorithms and methods to compute non-adiabatic couplings have emerged in the past decade. It is now understood that same-symmetry intersections play as important a role in non-adiabatic processes as symmetry-allowed intersections.

• Yarkony, David (1996). "Diabolical Conical Intersections". Reviews of Modern Physics. 68 (4): 985–1013. Bibcode:1996RvMP...68..985Y. doi:10.1103/RevModPhys.68.985.
• Baer, Michael (2006). Beyond Born–Oppenheimer: Electronic Nonadiabatic Coupling Terms and Conical Intersections. Wiley-Interscience. doi:10.1002/0471780081. ISBN 978-0-471-77891-2.
• Domcke, Wolfgang; Yarkony, David R.; Köppel, Horst (2004). Conical Intersections: Electronic Structure, Dynamics and Spectroscopy. Advanced Series in Physical Chemistry. Vol. 15. World Scientific. doi:10.1142/5406. ISBN 978-981-256-546-4.
• Domcke, Wolfgang; Yarkony, David R.; Köppel, Horst (2011). Conical Intersections: Theory, Computation and Experiment. Advanced Series in Physical Chemistry. Vol. 17. World Scientific. doi:10.1142/7803. ISBN 978-981-4313-45-2.
• Born–Oppenheimer approximation
• Potential energy surface
• Geometric phase
• Christopher Longuet-Higgins
• Diabatic Representation
• Jahn–Teller effect
• Avoided crossing
• Bond softening
• Bond hardening
• Vibronic coupling
• Surface hopping
• Ab initio multiple spawning

• Computational Organic Photochemistry
• Potential Energy Surfaces and Conical Intersections