Zweipol

Als einen Zweipol (auch Eintor oder engl. two-pole bzw. one-port genannt) bezeichnet man in der Elektrotechnik ein elektrisches Bauelement oder eine elektrische Schaltung mit zwei „Anschlüssen“ (Klemmen, Polen). Er lässt sich als Blackbox durch sein Klemmenverhalten charakterisieren, indem man sein inneres Wirkungsprinzip (bei elementaren Bauelementen) bzw. seine Schaltungsstruktur (bei verschalteten Netzwerken) analysiert. Diese im Allgemeinen recht komplizierte Strom-Spannungs-Beziehung vereinfacht sich durch verschiedene Einschränkungen seiner Eigenschaften – insbesondere die der Linearität – wesentlich und wird „praxistauglich“.

Erweiterungen des Zweipols sind neben dem Dreipol insbesondere der Vierpol (Zweitor) und noch allgemeiner das Mehrtor (n-Tor), dessen einzelnen Tore jeweils für sich als Zweipol betrachtet werden können.

Eigenschaften

Entsprechend ihrem Klemmenverhalten lassen sich für Zweipole folgende Eigenschaften definieren:

Ein Zweipol heißt zeitvariant, wenn sein Verhalten explizit von der Zeit abhängig ist. Praktisch geschieht das entweder durch Verschiebung des Arbeitspunktes durch ein äußeres Steuersignal oder durch Parameterresonanz.

Da diese Anwendung einen Sonderfall darstellt, werden in der Literatur (und auch im Folgenden) meist nur zeitinvariante Zweipole behandelt. Deren Verhalten und Parameter sind nicht von einem konkreten Zeitpunkt abhängig – sie besitzen keine „innere Uhr“.

Ein Zweipol heißt resistiv (statisch, speicherfrei), wenn er im Inneren keine Blindwiderstände besitzt bzw. diese (bei Gleichstrom oder Niederfrequenz) auf die benötigte Funktionalität keinen Einfluss haben. Sein Verhalten kann durch zeitunabhängige algebraische Gleichungen beschrieben werden. Abgesehen von Hystereseeffekten besitzt er „kein Gedächtnis“. Periodische Ströme und Spannungen haben gegeneinander keine Phasenverschiebung.

Nichtresistive Zweipole werden in der Literatur aufgrund der in ihnen enthaltenen Reaktanzen auch als reaktive oder speziell als induktive bzw. kapazitive Zweipole bezeichnet.

Ein Zweipol heißt linear, wenn sein Verhalten und seine Parameter nicht von der Größe der Spannungen und Ströme abhängen. Seine Beschreibung kann dann durch lineare algebraische oder lineare Differentialgleichungen erfolgen. Bei passiven Zweipolen gilt dann der Überlagerungssatz. Lineare zeitinvariante speicherfreie Zweipole sind wegen ihrer einfachen Beschreibung auf der Basis des ohmschen Gesetzes der übliche Gegenstand der Gleichstromtechnik, obwohl die allgemeineren nichtlinearen Zweipole für zum Erreichen der gewünschten Funktionalität der meisten elektronischen Baugruppen essenziell sind.
Aktive Zweipole geben in mindestens einem Betriebszustand im zeitlichen Mittel Energie über ihre Klemmen ab. Dazu besitzen sie eine innere elektrische Energiequelle. Sie repräsentieren die sogenannten Generatorzweipole.

Dagegen geben passive Zweipole in keinem Betriebszustand im zeitlichen Mittel elektrische Energie über ihre Klemmen ab. Als Verbraucherzweipole wandeln sie die aufgenommene Energie oft in eine andere Energieform um und geben diese beispielsweise als Wärmeenergie an die Umgebung ab. In den ebenfalls passiven, aber nur aus Blindwiderständen bestehenden Reaktanzzweipolen wird dagegen die Energie nur zwischengespeichert und geht im zeitlichen Mittel weder verloren noch wird neue erzeugt.

Nach ihrem grundsätzlichen inneren Aufbau unterscheidet man:

Zweipole aus konzentrierten Bauelementen, bei denen aufgrund ihrer Kompaktheit die interne Signallaufzeit keine Auswirkungen auf deren Verhalten hat:

Hierzu zählen sowohl elementare zweipolige Bauelemente, deren Verhalten durch ein physikalisches Ersatzschaltbild nachgebildet wird, als auch tatsächlich aus elementaren Bauelementen zusammengesetzte Netzwerke. Insbesondere passive lineare Zweipole aus konzentrierten Bauelementen teilt man weiter nach den ausschließlich verwendeten idealen Netzwerkelementen in RLC-, RC-, RL- und LC-Zweipole (letztere sind Reaktanzzweipole, die im Inneren keine Energie umsetzen) ein. Sie können durch gewöhnliche lineare Differentialgleichungen bzw. durch rationale Zweipolfunktionen beschrieben werden.

Zweipole aus verteilten Bauelementen, bei denen sich die internen Laufzeiten aufgrund ihrer Ausdehnung und der dadurch auftretenden Wellenerscheinungen auf das äußere Verhalten auswirken:

Passive lineare Zweipole aus verteilten Bauelementen sind beispielsweise die Eingänge von Lecherleitungen (verlustlos) und Antennen (verlustbehaftet durch Abstrahlung). Ihr Verhalten kann durch partielle lineare Differentialgleichungen bzw. durch eine nichtrationale Zweipolfunktion beschrieben werden.

Resistive Zweipole

Da resistive Zweipole (per Definition) keine Blindwiderstände besitzen bzw. diese bei Gleichstrom oder niedrigen Frequenzen vernachlässigt werden können, wird ihr Strom-Spannungs-Verhalten durch eine statische zeitunabhängige Beziehung geprägt. Grafisch und deshalb besonders anschaulich wird diese als Strom-Spannungs-Kennlinie dargestellt.

Bei konkreten Rechnungen und Darstellungen muss auf die Richtung von Strom- und Spannungspfeil an den Polen geachtet und entschieden werden, ob das Verbraucherzählpfeilsystem oder das Erzeugerzählpfeilsystem verwendet wird.

Falls überhaupt möglich, gibt es für die analytische Darstellung mehrere Varianten:

Implizite Darstellung: $f(u_{1},i_{1})=0$
Explizite Darstellung: $i_{1}=f(u_{1})$ oder $u_{1}=f(i_{1})$
Parameterdarstellung (mit dem Parameter $\lambda$ ): $u_{1}=f(\lambda )$ , $i_{1}=f(\lambda )$

Beispielsweise beschreibt man die Strom-Spannungs-Kennlinie einer Halbleiterdiode oft durch die Shockley-Gleichung

i_{1}=I_{\text{S}}\cdot \left(e^{\frac {u_{1}}{n\cdot U_{\text{T}}}}-1\right)

Die Kennlinie passiver resistiver Zweipole liegt (im Verbraucherzählpfeilsystem) nur im ersten und dritten Quadranten und geht durch den Nullpunkt. Sobald sie (teilweise) den zweiten oder vierten Quadranten durchläuft, ist der Zweipol aktiv, weil er beim Betrieb in diesen Arbeitspunkten dauernd Energie abgeben kann.

Die Kennlinie eines resistiven Zweipols kann sowohl unsymmetrisch (typisch für einzelne Halbleiterdioden) als auch symmetrisch (beispielsweise für ein Paar antiparallel geschalteter Dioden) sein.

Während die Kennlinie der meisten Zweipole monoton steigend bzw. fallend (und damit eindeutig) ist, gibt es einige Bauelemente (z. B. die Tunneldiode) und elektronische Schaltungen, die einen fallenden Kennlinienteil und damit einen negativen differentiellen Widerstand besitzen. Bezogen auf die Form dieser nichteindeutigen Kennlinie unterscheidet man strom- und spannungsgesteuerte resistive Zweipole. In besonderen Fällen kann die Kennlinie von resistiven Zweipolen Hysterese-Effekte beinhalten.

Die Analyse nichtlinearer resistiver Zweipole kann mit grafischen Methoden, nach erfolgter Kennlinienapproximation mit analytischen Methoden oder mit numerischen Methoden erfolgen. Nichtlineare resistive Zweipole können bei geringen Signalschwankungen, dem sogenannten Kleinsignalbetrieb, an stetigen Arbeitspunkten linearisiert und durch einen linearen Zweipol angenähert werden.^[1]

Lineare Zweipole

Lineare (zeitinvariante) Zweipole werden im Allgemeinen durch lineare Differentialgleichungen oder Differentialgleichungssysteme mit konstanten Koeffizienten beschrieben. Da diese in der Praxis schlecht handhabbar sind, werden sie durch Nutzung der komplexen Wechselstromrechnung, der Laplace-Transformation oder einer anderen Operatorenrechnung in lineare algebraische Gleichungen oder Gleichungssysteme umgewandelt. Damit können alle Methoden der Netzwerkanalyse der Gleichstromtechnik auch auf die Wechselstromtechnik und allgemein auf beliebige Signalformen ausgedehnt werden.

Wesentlich ist die dadurch entstehende Möglichkeit der Beschreibung des Klemmenverhaltens eines passiven linearen Zweipols durch seine Impedanz oder Admittanz. Beispielsweise lautet die Impedanz eines RLC-Reihenschwingkreises als Zweipol mit der imaginären Kreisfrequenz $j\omega$

{\underline {Z}}(j\omega )=R+j\omega L+{\frac {1}{j\omega C}}

Praktisch erfolgt die grafische Darstellung als frequenzabhängige Ortskurve oder als Betrags- und/oder Phasenfrequenzgang (beispielsweise im Bode-Diagramm).

Für die Zweipolsynthese ist die Verwendung der komplexen Frequenz $s=\sigma +j\omega$ günstiger, beispielsweise beim RLC-Reihenschwingkreis

{\underline {Z}}(s)=R+sL+{\frac {1}{sC}}=L\cdot {\frac {s^{2}+s\cdot {\frac {R}{L}}+{\frac {1}{LC}}}{s}}

Zweipole aus konzentrierten Bauelementen besitzen rationale (von der komplexen Frequenz $s$ abhängige) Impedanz- und Admittanzfunktionen, welche weitere einschränkende Eigenschaften besitzen. In der Literatur bezeichnet man diese „realisierbaren“ Funktionen als Zweipolfunktionen. Ihre grafische Darstellung erfolgt als PN-Diagramm.

Zweipole aus verteilten Bauelementen besitzen keine rationale Impedanz- oder Admittanzfunktion. Beispielsweise lautet die Impedanz eines kurzgeschlossenen verlustlosen Leitungsstücks mit dem (reellen) Wellenwiderstand $Z_{L}$ , der Phasengeschwindigkeit $v$ und der Länge $l$

{\underline {Z}}(s)=Z_{L}\cdot \tanh {\left(s\cdot {\frac {l}{v}}\right)}

Lineare resistive Zweipole

Die Strom-Spannungs-Kennlinie linearer resistiver Zweipole ist eine Gerade. Einfache Repräsentanten dieser Zweipole sind die Elemente des Grundstromkreises der linearen Elektrotechnik: Spannungs- oder Stromquelle als aktiver linearer Zweipol und der ohmsche Widerstand als passiver linearer Zweipol.

In der Literatur, der Lehre und im folgenden Abschnitt stehen sie stellvertretend für die Präsentation der Berechnung linearer Zweipole, da die Rechenregeln für die Gleichstromtechnik und die Wechselstromtechnik auf Basis der komplexen Wechselstromrechnung äquivalent sind (ohmsches Gesetz im komplexen Bereich).

Ersatzschaltungen linearer Zweipole

Wenn nur das Klemmenverhalten eines linearen Zweipols und nicht sein exakter interner Aufbau von Interesse ist, kann dieser durch eine kompaktere Ersatzschaltung dargestellt werden. Die Ersatzschaltung besitzt dabei das gleiche Strom-Spannungs-Verhalten an den Klemmen wie die ursprüngliche Schaltung.

Passive Zweipole

Stern-Dreieck-Transformation von Widerständen

Wenn Zweipole aus rein passiven Elementen bestehen, sind diese meist durch Kombinationen von Parallelschaltungen und Reihenschaltungen miteinander verschaltet und können leicht zusammengefasst werden. In seltenen Fällen kommt es jedoch vor, dass drei Elemente einen sogenannten Stern oder ein Dreieck bilden und ein direktes Zusammenfassen verhindern. Eine Stern-Dreieck-Transformation kann jedoch so eine Problemstelle auflösen, wodurch ein weiteres Zusammenfassen ermöglicht wird. Bilden mehr als drei Schaltelemente eine dieser Problemstellen, spricht man von Sternen und Polygonen sowie folglich der verallgemeinerten Stern-Polygon-Transformation.

Die Zweipolgleichung für passive Zweipole lautet:

U_{1}=R_{\text{Ersatz}}\cdot I_{1}

Aktive Zweipole

Ersatzspannungsquelle bzw. Thévenin-Äquivalent

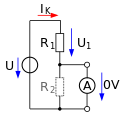
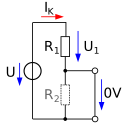
Eine Ersatzschaltung für einen aktiven Zweipol besteht aus einer Ersatzspannungsquelle oder Ersatzstromquelle sowie einem Innenwiderstand. Im Bild rechts ist ein einfacher Spannungsteiler als Beispiel für einen einfachen aktiven Zweipol aus einer Spannungsquelle U und zwei Widerständen R₁, R₂ in Reihenschaltung dargestellt. Die Ausgangsspannung U₂ fällt über die Parallelschaltung aus R₂ und einem eventuell angeschlossenen Lastwiderstand R_L ab. Der Wert der im nächsten Bild rechts gezeigten Ersatzspannungsquelle, die sogenannte Leerlaufspannung, kann am Ausgang im unbelasteten Zustand ohne R_L ( $R_{L}=\infty$ ) entweder mit einem Spannungsmessgerät gemessen oder über die Spannungsteilerregel bestimmt werden. Für das Beispiel ergibt sich der Wert der Ersatzspannungsquelle zu:

U_{2,LL}={\frac {R_{2}}{R_{1}+R_{2}}}\cdot U

Zur Bestimmung des Innenwiderstandes wird noch der Kurzschlussstrom benötigt. Dazu wird der Ausgang kurzgeschlossen ( $R_{L}=0$ ). Für eine Strommessung erfolgt dies mit einem Strommessgerät. Bei einer Berechnung stellt man fest, dass durch den Kurzschluss keine Spannung mehr über R₂ abfällt und sich folgender Kurzschlussstrom für das Beispiel ergibt:

I_{K}={\frac {U}{R_{1}}}

Mit beiden Werten ergibt sich der Innenwiderstand der Ersatzschaltung zu:

R_{i}={\frac {U_{2,LL}}{I_{K}}}={\frac {R_{1}\cdot R_{2}}{R_{1}+R_{2}}}=R_{1}\parallel R_{2}

Rein mathematisch ergibt sich diese Lösung für den Innenwiderstand auch, wenn die Spannungsquelle kurzgeschlossen und der Ausgang im Leerlauf ist. Von den Ausgangsklemmen aus betrachtet, entspricht der Innenwiderstand der Parallelschaltung der beiden Teilerwiderstände. Im zweiten Bild ist die Ersatzschaltung zu sehen.

Leerlaufspannung		Kurzschlussstrom		Innenwiderstand
Messung	Rechnung	Messung	Rechnung	Innenwiderstand
	$Mathematische Bestimmung von U2,LL$		$Mathematische Bestimmung von IK$

Der Lastwiderstand R_L bleibt von der Umstellung unbeeinflusst. Er bildet nun eine Reihenschaltung bzw. Spannungsteiler mit R_i und seine Wirkung auf die Ausgangsspannung tritt deutlich hervor. Je größer er ist ( $R_{L}\to \infty$ ), desto mehr nähert sich die Ausgangsspannung der Leerlaufspannung und der Ausgangsstrom geht gegen Null. Je kleiner er ist ( $R_{L}\to 0$ ), desto mehr nähert sich die Ausgangsspannung dem Wert 0 und der Ausgangsstrom dem Kurzschlussstrom. Die Ausgangsspannung in Abhängigkeit vom Ausgangsstrom drückt die Zweipolgleichung aus:

U_{2}=U_{2,LL}-R_{i}\cdot I_{L}

Die Ersatzschaltung kann nach dem Norton-Theorem in eine äquivalente Schaltung mit Ersatzstromquelle und Innenleitwert umgeformt werden. Die Zweipolgleichung abhängig von U₂ lautet dann:

I_{L}=I_{K}-G_{i}\cdot U_{2}

Leistung und Wirkungsgrad aktiver Zweipole

Die Ausgangsleistung wird bestimmt durch:

P_{L}=U_{2}\cdot I_{L}={\frac {R_{L}\cdot U_{2,LL}}{R_{i}+R_{L}}}\cdot {\frac {U_{2,LL}}{R_{i}+R_{L}}}={\frac {R_{L}}{(R_{i}+R_{L})^{2}}}\cdot U_{2,LL}^{2}

Die Gesamtleistung beträgt:

P_{\text{ges}}=U_{2,LL}\cdot I_{L}={\frac {1}{R_{i}+R_{L}}}\cdot U_{2,LL}^{2}

Der Wirkungsgrad wird berechnet durch:

\eta ={\frac {P_{L}}{P_{\text{ges}}}}={\frac {R_{L}}{R_{i}+R_{L}}}

Je größer R_L, desto größer ist der Wirkungsgrad. Er kann Werte zwischen 0 ( $R_{L}=0$ ) und 1 ( $R_{L}\to \infty$ ) annehmen. Bei Leistungsanpassung (maximal mögliche Verbraucherleistung) ( $R_{i}=R_{L}$ ) beträgt er 0,5.

Zweipoltheorie

Unter dem Begriff Zweipoltheorie versteht man in der elektrotechnischen Literatur^[2] (im Gegensatz zum Begriff der Vierpoltheorie) eine vereinfachte Analysemethode zur Ermittlung einer Spannung und/oder eines Stromes in einem komplizierten linearen elektrischen Netzwerk. Ihre Anwendung erfolgt in drei Schritten:

Das Netzwerk wird so in zwei Zweipole zerlegt, dass die gesuchte Spannung und/oder der gesuchte Strom gerade an den durch die Schnittstelle entstehenden Polen auftreten.
Mit Hilfe einer beliebigen Methode werden die Ersatzschaltungen der beiden Zweipole ermittelt.
Auf der Basis des entstandenen Grundstromkreises werden die gesuchten Größen aus den Parametern der ermittelten Ersatzschaltungen errechnet.

Zweipolsynthese

Die Zweipolsynthese stellt sich die Aufgabe, ausgehend von der Beschreibung des Klemmenverhaltens eines linearen (zeitinvarianten) RLC-Zweipols eine (dieses Klemmenverhalten realisierende) Netzwerkstruktur aus den elementaren passiven Elementen R, L und C durch algorithmisierbare Schritte systematisch zu berechnen. Üblicherweise sind solche Syntheselösungen nicht eindeutig und je nach verwendeter Synthesemethode erhält man unterschiedliche Schaltungsstrukturen. Die dafür benötigten theoretischen Grundlagen wurden im Wesentlichen schon in den 1920er und 1930er Jahren von Foster, Cauer und Brune gelegt.

Die Zweipolsynthese erfolgt in drei Schritten^[3]:

Aufgrund der Anforderungen an das gewünschte Klemmenverhalten des Zweipols erfolgt die Charakterisierung im Zeit- oder Frequenzbereich (praktisch meist als Ortskurve oder Frequenzgang des Betrags von Impedanz oder Admittanz).
Zum Erreichen der Realisierbarkeit muss eine Approximation erfolgen, um eine praktisch realisierbare sogenannte Zweipolfunktion zu erhalten. Dazu erfolgt eine Anpassung der Forderungen an ihre Realisierbarkeit entsprechend einem Gütekriterium. Eine solche Zweipolfunktion ist nur dann realisierbar, wenn sie rational von der komplexen Frequenz $s=\sigma +j\omega$ abhängt und eine sogenannte positive Funktion ist. Letzteres bedeutet, dass sie für reelle $s$ selbst reell ist und für $\sigma >0$ regulär ist sowie positiven Realteil besitzt (Brune 1931). Soll ein reiner Reaktanzzweipol entstehen, dann muss die Zweipolfunktion für rein imaginäre $s$ auch rein imaginäre Werte annehmen. Man spricht dann von einer Reaktanzfunktion.^[4]
Die ermittelte Zweipolfunktion wird geeignet umgeformt, um daraus die gewünschte Realisierung „abzulesen“. Für reine Reaktanzzweipole sind das beispielsweise die Partial- und Kettenbruchdarstellung. Auch für reine RL- und RC-Zweipole gibt es passende Bedingungen und Formen. Für die allgemeineren RLC-Zweipole ist beispielsweise der sogenannte Brune-Prozess eine typische Vorgehensweise.

Da Induktivitäten in der modernen Halbleitertechnik schlecht realisierbar sind, gibt es Methoden zur Synthese von aktiven RC-Zweipolen unter Nutzung von aktiven Bauelementen, beispielsweise gesteuerten Quellen, Operationsverstärkern, Negativimpedanzkonvertern und Gyratoren.^[5]

Literatur

Lorenz-Peter Schmidt, Gerd Schaller, Siegfried Martius: Grundlagen der Elektrotechnik 3. Netzwerke. Pearson Studium, München 2006, ISBN 3-8273-7107-4.

Einzelnachweise

↑ Reinhold Paul: Elektrotechnik 2 – Netzwerke. Springer-Verlag, Berlin Heidelberg New York 1994, ISBN 3-540-55866-7.
↑ Klaus Lunze: Einführung in die Elektrotechnik: Lehrbuch für Elektrotechnik als Hauptfach. Verlag Technik, Berlin 1991, ISBN 3-341-00980-9.
↑ Rolf Unbehauen: Netzwerk- und Filtersynthese: Grundlagen und Anwendungen. Oldenbourg Verlag, München - Wien 1993, ISBN 3-486-22158-2.
↑ Gerhard Wunsch: Geschichte der Systemtheorie (= Wissenschaftliche Taschenbücher: Texte und Studien. Band 296). Oldenbourg Verlag, München - Wien 1985, ISBN 3-486-29531-4.
↑ Peter Vielhauer: Lineare Netzwerke. Verlag Technik, Berlin 1982, DNB 830310258.

[1] Reinhold Paul: Elektrotechnik 2 – Netzwerke. Springer-Verlag, Berlin Heidelberg New York 1994, ISBN 3-540-55866-7.

[2] Klaus Lunze: Einführung in die Elektrotechnik: Lehrbuch für Elektrotechnik als Hauptfach. Verlag Technik, Berlin 1991, ISBN 3-341-00980-9.

[3] Rolf Unbehauen: Netzwerk- und Filtersynthese: Grundlagen und Anwendungen. Oldenbourg Verlag, München - Wien 1993, ISBN 3-486-22158-2.

[4] Gerhard Wunsch: Geschichte der Systemtheorie (= Wissenschaftliche Taschenbücher: Texte und Studien. Band 296). Oldenbourg Verlag, München - Wien 1985, ISBN 3-486-29531-4.

[5] Peter Vielhauer: Lineare Netzwerke. Verlag Technik, Berlin 1982, DNB 830310258.

[1]

[2]

[3]

[4]

[5]

Fahrer / Team für die Suche eingeben: