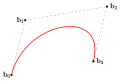
Typometrie (Typografie)

Die Typometrie beschreibt in der Typografie die geometrische Gestalt und die relativen Größenverhältnisse (Proportionen) von Schriftzeichen (Buchstaben, Ziffern und Sonderzeichen).[1] Die Typometrie gehört zur Mikrotypografie, auch „Detailtypografie“ genannt.[2]
Die Bezeichnung Typometrie wird seit 2003 von dem Typografen Wolfgang Beinert propagiert. Nach eigener Aussage hat er sie definiert und „in den typografischen Diskurs eingebracht“, weil sie „in der offiziellen Terminologie“ bislang gefehlt habe.[1] Beinerts Erläuterung zu seiner Wortschöpfung schließt einen Rückblick auf die Renaissance ein, in der die systematische Beschreibung der geometrischen Konstruktion von Buchstaben begann.[1] Entsprechend wird dieses Thema nachfolgend dargestellt.
Beispiel: Optimierung der Proportionen
Um einen optimalen optischen Eindruck zu erzeugen, stehen die Querstriche der Großbuchstaben nicht alle auf derselben Höhe und die Größe der Bögen variiert:[3]
- Beim A sollte der Querstrich etwas tiefer liegen als in der Mitte, beim E, F und H der Mittelstrich etwas höher.
- B und S sehen angenehm aus, wenn der oberen Bogen etwas kleiner ist als der untere.

Ein sogenannter Überhang entsteht durch die minimale Vergrößerung mancher Buchstaben, die ohne diese Größenkorrektur etwas zu klein aussehen würden (vgl. das Bild rechts).
- Ein e oder o mit unterem Überhang reicht minimal weiter nach unten als bis zur Grundlinie.
- Wenn bei einem i der Schaft oben spitz ausläuft, kann diese Spitze minimal über die x-Linie hinausreichen.
- Das p reicht an zwei Stellen minimal über die x-Linie hinaus: am spitzen oberen Ende des Schafts und an der oberen Rundung.
Historische Entwicklung
Antike Majuskeln

2. Jahrhundert v. Chr.
Die römischen Majuskeln (im „Zweiliniensystem“ mit Grund- und Oberlinie) bestehen geometrisch aus Geraden und Rundungen bzw. aus den Grundformen Quadrat, Dreieck, Kreis und Halbkreis.
- Römische Lapidarschrift: Capitalis monumentalis
- Schriftbeispiel für die Capitalis quadrata
Renaissance

Felice Feliciano
Angeregt von der Epigraphik der Römer und ihrer Capitalis monumentalis auf der Trajans-Säule entstanden seit der zweiten Hälfte des 15. Jahrhunderts erste systematische Anleitungen zur geometrisch exakten Konstruktion von Buchstaben. Die Kalligraphen orientierten sich am Vorbild der griechisch-römischen Majuskeln und oft auch an der proportio divina, der „göttlichen Proportion“ (Goldener Schnitt). Die erste Abhandlung zur typometrischen Konstruktion der römischen Kapitale ist das Alphabetum Romanum, ein Manuskript des italienischen Kalligraphen Felice Feliciano (Verona 1463, im Codex Vaticanus 6852[4]).[1]

Luca Pacioli
Zu Beginn des 16. Jahrhunderts konstruierte der italienische Mathematiker Luca Pacioli die Formen der Antiqua-Großbuchstaben durch Zeichnen von Linien und Kreisen.[5] Sein Werk Divina Proportione (1509)[6] enthält geometrische Darstellungen aller lateinischen Großbuchstaben. Er kann daher als Pionier der „mathematischen Typografie“ angesehen werden.[7] Pacioli strebte danach, die lateinischen Buchstaben römischer Inschriften und Grabsteine möglichst originalgetreu zu zeichnen.
Francesco Torniello

Francesco Torniello war ein Mailänder Typograf, der 1517 ein Werk mit dem Titel Opera del modo de fare le littere maiuscole antique[8] veröffentlichte, das ein Alphabet für lateinische Majuskeln vorstellte – zusammen mit geometrischen Hinweisen, wie die Buchstaben „mit Hilfe von Zirkeln für Kurven und einem Lineal“ (col circino in curvo e libella recta) konstruiert werden können. Zur Konstruktion des Buchstabens A schrieb er:
„Der Buchstabe A wird vom Quadrat geformt. Die Dicke des rechten Beins sollte ein Neuntel der Vertikalen betragen; es sollte außerhalb des Quadrats beginnen, wo es den Kreis berührt, der durch die oben liegende Horizontale einen halben Punkt links vom Mittelpunkt durchgeht, und in der unten liegenden Ecke des Quadrats endet mit den Kreisen, wie du sie eingezeichnet siehst. Alle äußeren Kreise haben einen Radius von einem Punkt und die inneren einen Radius von einem halben Punkt, gemessen von dem Mittelpunkt eines Kreises bis zu seinem Umfang. Das linke Bein sollte die halbe Dicke des rechten haben und die Innenlinie sollte einen Startpunkt haben, der mit der Mitte der oberen Linie des Quadrats zusammentrifft, und einen halben Punkt vor der Grundlinie enden, einen Punkt innerhalb der linken Vertikalen des Quadrats. Die Querlinie sollte ein Drittel der Dicke des rechten Beines aufweisen, wobei die obere Linie mit der Horizontalen in der Mitte des Quadrats zusammentreffen sollte.“[9]

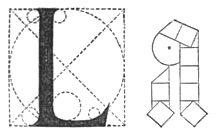
rechts: Dürers Textura-a
Albrecht Dürer
Während in Italien das Können bei den Formen der altrömischen („kapitalen“) Buchstaben wuchs, versuchte in Deutschland Albrecht Dürer dies bei der gotischen Schrift (Textura) – mit einheitlichen geometrischen Formen (kleinen Quadraten) – nachzuahmen.[5] Die geometrischen Konstruktionen von Buchstaben von Albrecht Dürer erschienen 1525 in der »Underweysung der messung mit dem zirckel un richtscheyt in Linien, ebenen und gantzen corporen«.
- Konstruktionen von Albrecht Dürer, A bis D
- Konstruktionen E bis L
- Konstruktionen M bis P
- Konstruktionen Q bis V
- Konstruktionen X, Y, Z
Weitere Typografen
Etwa zur selben Zeit wie Dürers Anleitung entstanden ähnliche Werke von Giovanni Battista Verini in Italien und von Geoffroy Tory in Frankreich.
- Der Buchstabe A
aus Verinis Werk Luminario, 1526 - Der Buchstabe A aus Geoffroy Torys Werk Champ Fleury, 1529

Verfeinerung des Rasters
Schon Francesco Torniello hatte 1517 ein 18×18-Raster beschrieben, das ihm bei der Konstruktion der Großbuchstaben als Koordinatensystem diente.[8]
Pierre Simon Fournier, der 1737 den „Punkt“ als typografische Maßeinheit einführte, verwendete ein wesentlich feineres Raster. Im Bild rechts ist zu sehen, wie Fournier den Buchstaben M in einem von ihm so genannten „großen Quadrat“ konstruiert, das in 64 „kleine Quadrate“ unterteilt ist, die jeweils aus 36 noch kleineren Quadraten bestehen. Die Rasterfläche des großen Quadrats besteht also aus 64 × 36 = 2304 (= 48 × 48) sehr kleinen Quadraten. In der kleinen Zeichnung links unten neben dem großen Quadrat mit dem M demonstriert Fournier eine noch feinere Unterteilung eines „kleinen Quadrats“ in 144 Teilflächen. Die Rasterfläche des großen Quadrats bestünde dann aus 64 × 144 = 9216 (= 96 × 96) sehr kleinen Quadraten.
Gegenwart
Seit der Personal Computer (ab 1995) und das Desktop Publishing (DTP) weitgehend den Bleisatz sowie den Fotosatz verdrängte, werden Buchstaben, Ziffern und Sonderzeichen fast nur noch mit Schrift-Editor-Programmen entworfen und generiert (z. B. mit Metafont, Fontographer oder FontForge). Um heute digitale Buchstaben (Fonts) herzustellen, sind keine kalligrafischen Fähigkeiten mehr nötig, aber „anatomische“ Kenntnisse des einzelnen Buchstabens mit seinem „Grundgerüst und Extremitäten“.[10]
Bei Rastergrafiken bestehen die Buchstaben aus einzelnen Pixeln, wie bei den Bitmaps in einfachen Grafikprogrammen. Die Schrifteditor-Programme erzeugen oder verändern die Buchstaben mit einer Vektorgrafik. Mit einer Vektorgrafik wird ein Buchstabe aus Linien, Polygonen (Vielecken), Kreisen oder Kurven (Splines oder Bézierkurven) zusammengesetzt.
- Vergleich: Outline- und Rastergrafik-Schriftart
- Bézier-Kurve 3. Grades und ihr Polygon
Literatur
- Albert Kapr: Schriftkunst. Geschichte, Anatomie und Schönheit der lateinischen Buchstaben. Verlag der Kunst, Dresden 1971.
- Hans Kühne: Schriftschule. Kallmeyer, Wolfenbüttel 1978.
- Joep Pohlen: Letterfontäne – Über Buchstaben. Taschen-Verlag, Köln 2011.
- Meyers Konversations-Lexikon Band 14: Schreibkunst. Verlag des Bibliographischen Instituts, Leipzig und Wien 1885 (4. Auflage).
Weblinks
- Typometrie im Typolexikon von Wolfgang Beinert
Siehe auch
Einzelnachweise
- ↑ a b c d Typometrie im Typolexikon von Wolfgang Beinert.
- ↑ Mikrotypografie im Typolexikon von Wolfgang Beinert.
- ↑ José M. Parramón: Das Handbuch der Schriften. Edition Michael Fischer, Stuttgart 1985, S. 24–32.
- ↑ Biblioteca apostolica vaticana: Manuscript – Cod. Vat. 6852
- ↑ a b Meyers Konversations-Lexikon (Band 14): Schreibkunst, Seite 626 f.
- ↑ Luca Pacioli: De Divina Proportione. Antonio Capella, Venedig 1509.
- ↑ Giovanni Mardersteig: The Alphabet of Francesco Torniello da Novara. Officina Bodoni, Verona 1971.
- ↑ a b Francesco Torniello da Novara: Opera del modo de fare le littere maiuscole antique. Gotardo da Ponte, Milano 1517.
- ↑ Hugo Kastner: Das Alphabet. Die Geschichte der Schrift. Marix Verlag, Schweinfurt 2012 (Leseprobe), Abschnitt A Aleph – Ochs.
- ↑ Claas Kalwa: Schrift-Anatomie schriftgestaltung.com