Ebene Welle

Eine ebene Welle ist eine Welle im dreidimensionalen Raum, deren Wellenfronten (d. h. Flächen gleichen Phasenwinkels) parallele Ebenen bilden. Die Ausbreitungsrichtung der Welle steht senkrecht dazu, ist also räumlich konstant.

Der Begriff wird fast ausschließlich für Wellen verwendet, die auch homogen und harmonisch sind, d. h. die mit zeitlich konstanter Frequenz einen sinusförmigen Verlauf zeigen, dessen Amplitude im ganzen Raum konstant ist. Solche Wellen gehören zu den einfachsten Lösungen der Wellengleichung, die in der klassischen Mechanik für elastische Verformungen sowie Druck- und Dichteschwankungen, in der Elektrodynamik für elektromagnetische Felder und in der Quantenmechanik für manche Materiewellen eine wichtige Rolle spielt.

Andere Lösungen der Wellengleichung sind die Kugelwelle (konzentrisch um einen Punkt) und die Zylinderwelle (konzentrisch um eine Gerade). Diese lassen sich in weiter Entfernung vom Zentrum in kleinen Bereichen gut durch eine ebene Welle annähern.

Das zweidimensionale Analogon zur ebenen Welle ist eine Welle, deren Wellenfronten gerade Linien sind, die sich auf einer ebenen Fläche bewegen. Ein anschauliches, aber nur näherungsweise^{[Anm. 1]} zutreffendes Beispiel sind die auf den Strand zulaufenden Ozeanwellen.

Homogene harmonische ebene Welle

Im nebenstehenden Bild ist der örtliche Verlauf einer harmonischen ebenen Welle gezeigt, die sich in x-Richtung ausbreitet und deren Größe A(x,t) in y-Richtung schwingt (ein Schnappschuss zum Zeitpunkt t=0). Die maximale Auslenkung (Amplitude) der Welle ist mit $A_{0}$ bezeichnet, ihre Wellenlänge mit $\lambda$ und ihre Phasenlage zu diesem Zeitpunkt mit $\varphi$ . Die Wellenlänge gibt die Periodizität von A im Raum an.

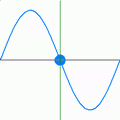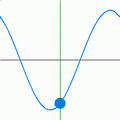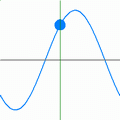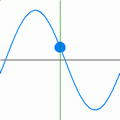
Ebene Sinuswelle, die in die negative x-Richtung läuft

Im nachfolgenden Bild ist der zeitliche Verlauf an einem festen Ort als Animation dargestellt. Die Frequenz $f=1/T$ ist ein Maß für die Periodizität von A in der Zeit. Die Phasengeschwindigkeit c gibt das Verhältnis aus räumlicher Periode $\lambda$ und zeitlicher Periode T an:

c={\frac {\lambda }{T}}=\lambda \cdot f

Eine ebene Welle wird am einfachsten beschrieben, wenn das Koordinatensystem so gewählt wird, dass eine Achse ihrer Ausbreitungsrichtung entspricht. In den Richtungen senkrecht zur Ausbreitung findet keine Schwingung statt.

Somit lässt sich eine harmonische homogene ebene Welle darstellen als

{\begin{aligned}A(x,t)&=A_{0}\cdot \sin \left[2\pi f\left({\frac {x}{c}}-t\right)+\varphi \right]\\&=A_{0}\cdot \sin \left[\omega \left({\frac {x}{c}}-t\right)+\varphi \right]\end{aligned}}

mit der Kreisfrequenz $\omega$ .

Bei dieser bewegen sich die Punkte konstanter Phase mit der Phasengeschwindigkeit c in die positive x-Richtung. In der inneren Klammer kompensiert das Anwachsen von x/c gerade das der Zeit t, so dass

{\frac {x}{c}}-t=\mathrm {const} \Leftrightarrow c={\frac {x}{t}}+\mathrm {const} '

eine Ebenengleichung für die Wellenfront darstellt.

Für eine Richtungsumkehr, wie sie etwa durch Reflexion an einer Inhomogenität im Medium auftritt (z. B. Änderung von Brechungsindex oder Schallkennimpedanz), ist das Vorzeichen von x oder die x-Achse selbst umzudrehen.

Die Physik der sich periodisch ändernden Größe A ist für das Konzept der ebenen Welle unwichtig. Es kann sich um eine mechanische Auslenkung, eine Druckänderung, eine Feldstärke oder etwa eine Wahrscheinlichkeitsamplitude handeln. Falls es sich um eine vektorielle Größe handelt, gibt die Richtung ihrer Amplitude ${\vec {A}}_{0}$ relativ zur Ausbreitungsrichtung ihre Polarisation an.

Allgemeine Form einer ebenen Welle

In allgemeiner Form ist eine ebene Welle einer physikalischen Größe $A$ gegeben durch:

A({\vec {x}},t)=f\left({\vec {n}}\cdot {\frac {\vec {x}}{c}}-t\right)

Darin ist

$f(\tau )$ eine beliebige (skalare oder vektorwertige) Funktion, die nicht notwendig periodisch sein muss
$|{\vec {n}}|=1$ der Einheitsvektor in Ausbreitungsrichtung.

Die Welle pflanzt sich in Richtung ${\vec {n}}$ fort mit der Geschwindigkeit c.

Beobachtet man die Welle an einem festen Ort ${\vec {x}}$ , so ändert sich die betrachtete Größe $A$ zeitlich gemäß der Funktion $f$ .

Die Schwingungsphase ist gegeben durch:

{\vec {n}}\cdot {\frac {\vec {x}}{c}}-t

Die Punkte gleicher Schwingungsphase bilden eine Ebene, die auf dem Vektor ${\vec {n}}$ senkrecht steht.

Bei der physikalischen Größe $A$ kann es sich handeln um:

einen Skalar, z. B. den Druck
einen Vektor, z. B. die räumliche Auslenkung aus einer Ruhelage
ein Kraftfeld.

Bei vektoriellen Wellen kann man unterscheiden:

die longitudinale Polarisation: Vektor ${\vec {A}}$ liegt parallel zur Ausbreitungsrichtung ${\vec {n}}$
die transversale Polarisation: Vektor ${\vec {A}}$ liegt senkrecht zur Ausbreitungsrichtung ${\vec {n}}$ .

Die ebene Welle ist eine Lösung der Wellengleichung:

\nabla ^{2}A-{\frac {1}{c^{2}}}{\frac {\partial ^{2}A}{\partial t^{2}}}=0

mit

dem Nabla-Operator $\nabla$
der partiellen Ableitung nach der Zeit ${\frac {\partial }{\partial t}}$ .

In der Praxis werden nur harmonische ebene Wellen verwendet, da jede allgemeine ebene Welle als Summe harmonischer ebener Wellen dargestellt werden kann (Fourier-Analysis). Dies liegt daran, dass man die allgemeine Form der ebenen Welle A als Fourierintegral darstellen kann:

{\begin{aligned}f(\tau )&=\mathrm {Re} \int _{0}^{\infty }\phi (\omega )\cdot e^{i\tau \omega }\,\mathrm {d} \omega \\&={\frac {1}{2}}\left(\int _{0}^{\infty }\phi (\omega )\cdot e^{i\tau \omega }\,\mathrm {d} \omega +\int _{0}^{\infty }\phi ^{*}(\omega )\cdot e^{-i\tau \omega }\,\mathrm {d} \omega \right)\end{aligned}}

mit der imaginären Einheit $i$ .

Dies entspricht einer Summe über harmonische ebene Wellen mit kreisfrequenzabhängigen Amplituden $\phi (\omega )$ . Hier wird nur der physikalisch sinnhafte Realteil der Fouriertransformation betrachtet und im letzten Teil der Gleichung mithilfe der Identität

\mathrm {Re} (a)={\frac {1}{2}}(a+a^{*})

mit der komplexen Konjugation * dargestellt.

Harmonische ebene Welle

Aufgrund der Gültigkeit des Superpositionsprinzips für die Wellengleichung reicht es nun für weitere Betrachtungen, nur die spektrale Komponente der Kreisfrequenz $\omega$ zu betrachten:

{\begin{aligned}g(\omega ,t,x,y,z)&=\phi (\omega )\cdot \exp(i\,\omega \,\tau )\\&=\phi (\omega )\cdot \exp \left[i\,\omega \left({\vec {n}}\cdot {\frac {\vec {x}}{c}}-t\right)\right]\end{aligned}}

g wird harmonische ebene Welle genannt.

Üblicherweise wird diese Form noch ausgedrückt mit Hilfe des Wellenvektors ${\vec {k}}$ :

{\vec {k}}=(k_{x},k_{y},k_{z})^{T}={\frac {\omega }{c}}\,{\vec {n}}

bzw. der Kreiswellenzahl $k$ :

k:=\left|{\vec {k}}\right|={\frac {\omega }{c}}={\frac {2\pi }{\lambda }}={\frac {2\pi \,f}{c}}

als

g(\omega ,t,x,y,z)=\phi (\omega )\cdot \exp \left[i\left({\vec {k}}\cdot {\vec {x}}-\omega \cdot {t}\right)\right]

Mit

\omega \cdot t=\pi /2

(im Bogenmaß),

\phi (\omega )=A_{0}

und

e_{i\cdot \varphi }=\cos(\varphi )+i\cdot \sin(\varphi )

entspricht der Realteil der harmonischen ebenen Welle der weiter oben eingeführten sinusförmigen ebenen Welle.

Inhomogene ebene Welle

Eine ebene Welle ist immer eine Lösung der Helmholtzgleichung (zeitliche Fouriertransformation der Wellengleichung):

\nabla ^{2}A+k^{2}(\omega )A=0

mit realer Dispersionsrelation $k(\omega )$ .

Die Helmholtzgleichung wird auch gelöst, wenn man für den Wellenvektor komplexe Komponenten zulässt:

{\vec {k}}={\vec {\beta }}+i{\vec {\alpha }}

Damit die Helmholtzgleichung erfüllt bleibt, muss aber das Quadrat $k^{2}(\omega )={\vec {k}}\cdot {\vec {k}}$ der Wellenzahl real bleiben, was auf folgende Bedingung führt:

{\begin{aligned}\mathrm {Im} (k^{2})&=0\\\Leftrightarrow \mathrm {Im} [({\vec {\beta }}+i{\vec {\alpha }})\cdot ({\vec {\beta }}+i{\vec {\alpha }})]&=0\\\Leftrightarrow \alpha _{x}\beta _{x}+\alpha _{y}\beta _{y}+\alpha _{z}\beta _{z}&=0\end{aligned}}

und eine Einschränkung der Wahl des komplexen Wellenvektors bedeutet. Diese Bedingung bedeutet anschaulich, dass der Realteil ${\vec {\beta }}$ des Wellenvektors senkrecht zu seinem Imaginärteil ${\vec {\alpha }}$ stehen muss.

Eine Welle der Form

A(x,t)=\int _{0}^{\infty }\phi (\omega )\exp \left[i({\vec {\beta }}{\vec {x}}-\omega t)-({\vec {\alpha }}{\vec {x}})\right]\mathrm {d} \omega

wird inhomogene ebene Welle oder nicht uniforme ebene Welle^[1] genannt. Sie breitet sich in die Richtung ${\vec {\beta }}$ aus, und ihre Amplitude fällt senkrecht zur Ausbreitungsrichtung ab (vgl. Abb.). Im Gegensatz zur homogenen ebenen Welle stehen hier die Ebenen konstanter Amplitude senkrecht zu den Ebenen konstanter Phase. Außerdem ist die Phasengeschwindigkeit immer geringer als bei einer homogenen ebenen Welle gleicher Frequenz.^[2]^[3]

Absorption

Wählt man Real- und Imaginärteil des komplexen Wellenvektors als parallele Vektoren, so ist der Imaginärteil $\alpha$ der Wellenzahl nicht wie im vorherigen Abschnitt Null, und die Wellenzahl wird komplex:

k=\beta +i\alpha

mit

dem Absorptionskoeffizient $\alpha$ (auch Dämpfungskonstante genannt)
der Phasenkonstante $\beta$ .

Dies führt auf eine gedämpfte harmonische ebene Welle. Legt man die x-Achse in Ausbreitungsrichtung, so folgt:

g(\omega ,t,{\vec {x}})=\phi (\omega )\,\mathrm {e} ^{i(\beta x-\omega t)}\,\mathrm {e} ^{-\alpha x}

Die Ebenen konstanter Phase und konstanter Amplitude sind identisch, nur die Amplitude nimmt in Ausbreitungsrichtung exponentiell ab (Faktor $\mathrm {e} ^{-\alpha x}$ ).^[4] Es handelt sich also um eine homogene ebene Welle.

Idealisierung

Eine ebene Welle füllt immer einen unendlich ausgedehnten Raum aus und ist somit eine Idealisierung der realen Welle. Denn einerseits kann keine ebene Welle von einem endlich ausgedehnten Sender abgestrahlt werden und andererseits ist die Energie einer ebenen Welle unendlich. Beides ist unphysikalisch.

Anmerkung

↑ Wasserwellen verringern (bei gleichbleibender Frequenz) ihre Fortpflanzungsgeschwindigkeit und Wellenlänge, wenn die Wassertiefe abnimmt, und verändern daher ihre ohnehin meist nicht sinusförmige Form bis hin zum Brecher.

Siehe auch

Partialwellenentwicklung

Weblinks

Commons: Ebene Welle – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

↑ G.S. Smith: An Introduction to Classical Electromagnetic Radiation. Cambridge University Press, 1993, S. 179 (eingeschränkte Vorschau in der Google-Buchsuche).
↑ ^:4 Inhomogene ebene Wellen können bei Brechung oder Reflexion in einfache ebene Wellen übergehen und umgekehrt. Sie existieren aber nur in beschränkten Räumen und nicht wie die einfache ebene Welle auch im unendlichen $\mathbb {R} ^{3}$ . Die Begründung dafür ist wie folgt: Die Amplitude der inhomogenen ebenen Welle nimmt in eine Richtung exponentiell ab, das aber ist gleichbedeutend mit einem exponentiellen Anwachsen in der Gegenrichtung. Dies führt in einem unbeschränkten Raum zu einer unendlichen Leistungsdichte und ist unphysikalisch.
↑ G.D. Durgin: Space-Time Wireless Channels. Prentice Hall Professional, 2003, S. 78–79 (eingeschränkte Vorschau in der Google-Buchsuche).
↑ G. Lehner: Elektromagnetische Feldtheorie. Springer, 2008, S. 436 (eingeschränkte Vorschau in der Google-Buchsuche).

[1] Wasserwellen verringern (bei gleichbleibender Frequenz) ihre Fortpflanzungsgeschwindigkeit und Wellenlänge, wenn die Wassertiefe abnimmt, und verändern daher ihre ohnehin meist nicht sinusförmige Form bis hin zum Brecher.

[2] G.S. Smith: An Introduction to Classical Electromagnetic Radiation. Cambridge University Press, 1993, S. 179 (eingeschränkte Vorschau in der Google-Buchsuche).

[brekhovskikh1-3] :4 Inhomogene ebene Wellen können bei Brechung oder Reflexion in einfache ebene Wellen übergehen und umgekehrt. Sie existieren aber nur in beschränkten Räumen und nicht wie die einfache ebene Welle auch im unendlichen $\mathbb {R} ^{3}$ . Die Begründung dafür ist wie folgt: Die Amplitude der inhomogenen ebenen Welle nimmt in eine Richtung exponentiell ab, das aber ist gleichbedeutend mit einem exponentiellen Anwachsen in der Gegenrichtung. Dies führt in einem unbeschränkten Raum zu einer unendlichen Leistungsdichte und ist unphysikalisch.

[4] G.D. Durgin: Space-Time Wireless Channels. Prentice Hall Professional, 2003, S. 78–79 (eingeschränkte Vorschau in der Google-Buchsuche).

[5] G. Lehner: Elektromagnetische Feldtheorie. Springer, 2008, S. 436 (eingeschränkte Vorschau in der Google-Buchsuche).

[Anm. 1]

[1]

[2]

[3]

[4]

Fahrer / Team für die Suche eingeben: