Stoßmittelpunkt

Der Stoßmittelpunkt und der Schwingungsmittelpunkt sind in der Mechanik identische Punkte eines festen Körpers. Fasst man den Stiel eines Hammers oder Beils im Stoßmittelpunkt, dann muss die Hand beim Hämmern keinen Prellstoß aushalten. Gewöhnlich ist der Stiel so lang, dass sich der Stoßmittelpunkt an seinem Ende befindet.^[1]^:525 Reduziert man andererseits den aufgehängten Körper auf einen Massenpunkt im Schwingungsmittelpunkt, dann hat dieses sogenannte mathematische Pendel dieselbe Schwingungsdauer wie der ursprüngliche Körper.^[1]^:447

Der Schwingungsmittelpunkt wird gelegentlich auch Oszillationszentrum genannt, anlehnend an die englische, französische und lateinische Namensgebung (center of oscillation, centre d’oscillation und centrum oscillationis).

Von Mitte des 17. bis Mitte des 18. Jahrhunderts nahm die Theorie des Schwingungsmittelpunktes neben der Theorie der Stoßgesetze einen zentralen Platz in der Erforschung der sich erst herausbildenden Klassischen Mechanik ein. Mit ihr entwickelten sich die Grundgesetze der Dynamik. Im Anschluss und bis heute wird sie als eine Anwendung der Eulerschen Gleichungen für starre Körper verstanden.^{[Anm. 1]}

Beschreibung

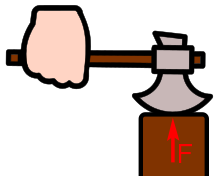
Wenn ein Beil auf einen Klotz prallt, übt dieser eine Reaktionskraft auf das Beil aus, siehe Abbildung 1. Die Reaktionskraft F tendiert dazu

einerseits das Beil nach oben zu beschleunigen und
andererseits das Beil in Drehung gegen den Uhrzeigersinn zu versetzen.

Durch die Beschleunigung nach oben bewegt sich der Endpunkt des Griffes nach oben und durch die Drehung senkt sich der Endpunkt ab. Für die Hand wäre es am angenehmsten, wenn der Griff dort, wo die Hand ihn hält, weder nach oben noch nach unten beschleunigt würde, sodass er keine Kraft auf die Hand ausübt. Der Punkt, wo dies der Fall ist, ist der Stoßmittelpunkt.

Voraussetzung war, dass das Beil symmetrisch zur Bildebene ist und die Stoßkraft F in ihr wirkt, damit das Beil durch den Stoß nicht senkrecht zur Bildebene kippt. Für den Stoßmittelpunkt ist nur die Kraftkomponente senkrecht zum Griff von Bedeutung. Eine Kraftkomponente in Richtung des Griffs ist sicherlich unangenehm und kann vermieden werden, indem dafür gesorgt wird, dass der Griff zum Zeitpunkt des Aufpralls auf den Klotz wie im Bild senkrecht zur Stoßkraft F, also waagerecht ausgerichtet ist.

Neben der Ausnutzung bei Beil und Hammer sind folgende Anwendungen bemerkenswert:

Wird eine Billardkugel auf einer glatten Ebene in ihrem Stoßmittelpunkt angestoßen, dann rollt sie auf der Ebene schlupflos ab, siehe Eulersche Kreiselgleichungen.
Wenn ein Körper mit Symmetrieebene, wie besagtes Beil und der Hammer, das Pendel eines Schlagwerkes, der Glockenklöppel oder das ballistische Pendel in seinem Stoßmittelpunkt aufgehängt wird, dann erfährt die Drehachse keinen Stoßdruck.^[1]^:525
Insbesondere wenn eine aufklappende Tür durch einen Türstopper bei 2/3 ihrer Breite aufgehalten wird, werden die Türangeln nur minimal belastet, siehe das Beispiele mit B≈0. Die hier vernachlässigte Elastizität der Tür führt zu Biegeschwingungen und Lagerreaktionen, die nur bei schwungvollem Aufschlag beachtenswert sind.

Stoßmittelpunkt

Betrachtet wird ein fester Körper, der in einem Punkt P frei drehbar aufgehängt ist. Der Einfachheit halber soll der Körper eine Symmetrieebene besitzen, in der der Massenmittelpunkt S, das Lager P und die Wirkungslinie der Stoßkraft F liegen. Dann führt der Körper eine ebene Bewegung aus, wo sich alle Körperpunkte in Parallelebenen aufhalten, siehe Abbildung.

Auf den nach unten hängenden Körper soll im Punkt C in der Symmetrieebene, exzentrisch eine Kraft F horizontal so wirken, dass bei der einsetzenden Drehbewegung der Lagerpunkt P in Ruhe bleibt, keine horizontale Lagerreaktion auftritt und sich die einsetzende Bewegung als reine Drehung um P darstellt. Würde man den Körper im Punkt P halten, würde die Stoßkraft, wie beim Beil oben, keine spürbare Wirkung auf die Hand ausüben. P ist dann der anfängliche Momentanpol,^[1]^:525 und es gilt:

{\mathsf {|PC|=r+e=r+{\frac {\theta _{S}}{mr}}}}

oder

{\mathsf {|SC|=e={\frac {\theta _{S}}{mr}}}}

mit:

m:	Masse des Körpers
r:	Abstand des Schwerpunkts vom Stützpunkt (│PS│)
θ_S:	Massenträgheitsmoment des Körpers um den Massenmittelpunkt S und eine Drehachse senkrecht zur Schwingungsebene.

Für die Herleitung wird eine Kraft betrachtet, die nicht im Massenmittelpunkt des Körpers angreift und ihn somit in Drehung versetzt. Der Kraftangriffspunkt soll so gewählt werden, dass die Drehung um den Schwerpunkt S dieselbe Winkelbeschleunigung ${\ddot {\alpha }}$ (zweifache Zeitableitung von α) erfährt wie die Drehung um den Aufhängepunkt P, denn das ist Voraussetzung dafür, dass sich der Körper um P dreht. Dann gilt der Drallsatz in der xy-Ebene:

{\mathsf {{\vec {M}}={\vec {r}}\times {\vec {F}}=\theta \cdot {\ddot {\vec {\alpha }}}}}

.

In Worten: „Drehmoment Kraft mal Hebelarm um einen Punkt ist gleich Massenträgheitsmoment um diesen Punkt mal Winkelbeschleunigung“. Auf diese Geometrie angewendet, ergibt sich für die Punkte P und S mit der angreifenden Kraft F und dem Massenträgheitsmoment θ_P des Körpers um P:

{\mathsf {(r+e)F=\theta _{P}{\ddot {\alpha }}\quad {\text{und}}\quad eF=\theta _{S}{\ddot {\alpha }}\quad \rightarrow \quad {\ddot {\alpha }}={\frac {(r+e)F}{\theta _{P}}}{\stackrel {!}{=}}{\frac {eF}{\theta _{S}}}}}

Der Steiner’sche Satz ${\mathsf {\theta _{P}=mr^{2}+\theta _{S}}}$ führt auf besagtes^[1]^:525^[2]

{\mathsf {|PC|=r+e=r+{\frac {\theta _{S}}{mr}}}}

oder

{\mathsf {|SC|=e={\frac {\theta _{S}}{mr}}}}

Schwingungsmittelpunkt

Betrachtet wird derselbe Körper, der im Punkt P unverschieblich aber drehbar aufgehängt wird. Die Gewichtskraft mg greift in seinem Schwerpunkt S an. Wenn dieser, wie in der Abbildung, nicht lotrecht unter oder über P liegt, übt die Gewichtskraft ein Drehmoment aus, das den Körper zum Pendeln anregt. Bei kleinen Schwingungen hat dieses sogenannte physikalische Pendel die Kreisfrequenz

{\mathsf {\omega _{p}^{2}={\frac {rmg}{\theta _{P}}}}}

mit:

r:	Abstand des Schwerpunkts vom Stützpunkt (│PS│)
m:	Masse des Körpers
g:	Schwerebeschleunigung und
θ_P:	Massenträgheitsmoment des Körpers um P und eine Drehachse senkrecht zur Schwingungsebene.

Beim mathematischen Pendel mit Massenpunkt in C ist die Kreisfrequenz nur vom Abstand |PC|=r+e der Masse vom Lager und nicht von der Masse selbst abhängig:

{\mathsf {\omega _{m}^{2}={\frac {g}{r+e}}}}

Hier ist |SC|=e der Abstand des Massenpunkts vom Schwerpunkt und die Länge |PC| wird auch reduzierte Länge genannt.^[1]^:447 Der Schwingungsmittelpunkt C liegt dort, wo beide Kreisfrequenzen übereinstimmen:

{\mathsf {\omega _{p}^{2}={\frac {rmg}{\theta _{P}}}=\omega _{m}^{2}={\frac {g}{r+e}}\quad \rightarrow \quad |PC|=r+e={\frac {\theta _{P}}{mr}}}}

Nach dem Steiner’schen Satz sind die Trägheitsmomente um P und S durch ${\mathsf {\theta _{P}=mr^{2}+\theta _{S}}}$ verknüpft, sodass sich wie beim Stoßmittelpunkt

{\mathsf {|PC|=r+e={\frac {mr^{2}+\theta _{S}}{mr}}=r+{\frac {\theta _{S}}{mr}}}}

oder

{\mathsf {|SC|=e={\frac {\theta _{S}}{mr}}}}

ergibt.^[1]^:447

Die Schwingungsdauer eines physikalischen Pendels ändert sich nicht, wenn Aufhängepunkt und Schwingungsmittelpunkt vertauscht werden.^[1]^:448

Mathematisches Pendel

Das mathematische Pendel besteht aus einem Massenpunkt, der im Schwerefeld an einem masselosen Faden aufgehängt ist. Beim Massenpunkt stimmen Schwerpunkt und Massenmittelpunkt überein und relativ zu ihnen hat der Punkt kein Massenträgheitsmoment (θ_S=0). Beim mathematischen Pendel stimmen deshalb Schwerpunkt, Massenmittelpunkt, Stoß- und Schwingungsmittelpunkt überein.

Beispiele

1. Der Balken

Betrachtet wird der in Abbildung 2 und Abbildung 3 dargestellte, an einem Ende aufgehängte Balken. Er besitzt einen rechteckigen Querschnitt mit Breite B und Höhe H senkrecht zur Bildebene, die Länge R=2r und die Masse m. Ein solcher Balken hat das Massenträgheitsmoment θ_S=m(R²+B²)/12 um den Massenmittelpunkt, siehe Liste von Trägheitstensoren, Parallelogramm und Quader. Der Stoß- und Schwingungsmittelpunkt befindet sich damit im Abstand

{\mathsf {|PC|=r+e=r+{\frac {\theta _{S}}{mr}}=r+{\frac {m(R^{2}+B^{2})}{12mr}}=r+{\frac {4r^{2}+B^{2}}{12r}}={\frac {4}{3}}r+{\frac {B^{2}}{12r}}}}

von einem Ende des Balkens. Mit B=r/2=R/4 wie in den Bildern ist

{\mathsf {|PC|=r+e={\frac {4}{3}}r+{\frac {B^{2}}{12r}}={\frac {65}{48}}r=1{,}3541{\bar {6}}\,r}}

oder

{\mathsf {|SC|=e=0{,}3541{\bar {6}}\,r}}

Beim dünnen Balken mit vernachlässigbarer Dicke B, wie bei einer Tür, ist

{\mathsf {|PC|=r+e={\frac {4}{3}}r={\frac {2}{3}}R}}

bzw.

{\mathsf {|SC|=e={\frac {r}{3}}={\frac {R}{6}}}}

2. Starr verbundene Punktmassen: das zusammengesetzte Pendel

Der einfachste Fall eines ausgedehnten Körpers, bei dem Stoß- bzw. Schwingungsmittelpunkt C nicht mit dem Massenmittelpunkt S zusammenfällt, betrifft zwei Körper A und B mit den Massen ${\mathsf {m_{A}}}$ und ${\mathsf {m_{B}}}$ . Sie werden an einer als masselos angenommenen Stange aufgehängt (siehe Abb. „Punktmassen“ links). Gesucht ist dann der Punkt C dieses zusammengesetzten Pendels.^{[Anm. 2]} Vom Aufhängungspunkt P aus betrachtet ist das Trägheitsmoment ${\mathsf {\theta _{P}=m_{A}a^{2}+m_{B}b^{2}}}$ . Und der Schwerpunkt der zwei Körper im Abstand ${\mathsf {r}}$ ergibt sich aus dem Ansatz ${\mathsf {m\cdot r=m_{A}a+m_{B}b}}$ , wenn ${\mathsf {m=m_{A}+m_{B}}}$ die Gesamtmasse des zusammengesetzten Pendels definiert. Dann folgt durch Einsetzung der Schwingungsmittelpunkt

{\mathsf {|PC|={\frac {m_{A}a^{2}+m_{B}b^{2}}{m_{A}a+m_{B}b}}}}

.

Für ein zusammengesetztes Pendel mit vier Massepunkten (siehe Abb. „Punktmassen“ rechts) in den Abständen ${\mathsf {(d_{1},d_{2},d_{3},d_{4})}}$ ergibt sich entsprechend der Schwingungsmittelpunkt von P aus als ${\mathsf {|PC|={\frac {m_{D_{1}}\cdot d_{1}^{2}+\ldots +m_{D_{4}}\cdot d_{4}^{2}}{m_{D_{1}}\cdot d_{1}+\ldots +m_{D_{4}}\cdot d_{4}}}}}$ . Und allgemein für ${\mathsf {n}}$ Massen in den Abständen ${\mathsf {(d_{1},\ldots d_{n})}}$ folglich

{\mathsf {|PC|={\frac {\sum _{1}^{n}m_{i}\cdot d_{i}^{2}}{\sum _{1}^{n}m_{i}\cdot d_{i}}}}}

.

Im infinitesimalen Übergang ${\mathsf {n\rightarrow \infty }}$ für unendlich viele Punktmassen ${\mathsf {\Delta m_{i}}}$ , die in einer Reihe angeordnet gedacht werden, muss der obige Fall in den eines dünnen starren Balkens (siehe obiges Beispiel 1) bzw. einer in der Ebene betrachteten Stange übergehen. Denn dies entspricht (bei homogen angenommener Massenverteilung ${\mathsf {\rho }}$ ) dem Übergang zu einem Massenkontinuum in einer Richtung ${\mathsf {x}}$ . Somit

{\mathsf {lim_{\Delta m\rightarrow 0}\Delta m=lim_{\Delta x\rightarrow 0}(\rho \cdot \Delta x)}}

.

Es folgt also durch Einsetzung im Grenzgang

{\mathsf {|PC|={\frac {\rho \cdot \int _{R}x^{2}\,dx}{\rho \cdot \int _{R}x\,dx}}={\frac {1/3\,R^{3}}{1/2\,R^{2}}}={\frac {2}{3}}R}}

(oder auch $l_{r}={\frac {2}{3}}l$ wie im Beispiel zum physikalischen Pendel gezeigt).

Entstehungsgeschichte

Die ursprüngliche Problemstellung zum Stoßmittelpunkt findet sich in der Mechanik Bernardino Baldis von 1621. Demnach wäre es eine schöne Fragestellung, an welcher Stelle eine einschlagende Axt oder ein Schwert die maximale Wirkung auf den geschlagenen Körper ausübt.^[3] Zugleich bemerkt Baldi die instantane Verschiebung dieser Stelle beim Übergang vom translativen Stoß im Schwerpunkt hin zur Rotation außerhalb des Schwerpunktes. Von Beginn an wird das Problem mechanisch mit einer internen Hebelwirkung erklärt. Unter Baldis Erklärung mischt sich allerdings auch ein spukhafter immaterieller Verschiebungsfluss.

Es war Marin Mersenne, der die Problemstellung 1644 in seinem Tractatus Mechanicus aufgreift und erstmals klar definiert. Er sorgte für ihre Verbreitung unter den mathematischen Gelehrten seiner Zeit und regte experimentelle Lösungen an. Nach ihm wurden nur noch mathematische Modelle als wissenschaftliche Erklärung anerkannt.^[4]

1. Definition: Ein Körper sei an einer Seite außerhalb seines Schwerpunktes festgestellt und erzeuge so eine Drehbewegung. Gesucht ist derjenige Punkt des Körpers, an dem die maximale „Stoßkraft“ (im Sinne der damaligen Quantitas motus) übertragen wird.

2. Definition: Auf experimentellem Weg verbindet Mersenne damit zugleich den Schwingungsmittelpunkt eines sog. Funependules, eines mathematischen Fadenpendels.^{[Anm. 3]}

3. Definition: Die Vorstellung, dass der Stoßmittelpunkt eines rotierenden Körpers keine Reaktionswirkung, keinen Prellstoß am Aufhängungspunkt zeigt, liegt indirekt bereits dem Hebelprinzip, angewendet auf eine Drehbewegung, zugrunde und ist implizit von Anfang an dabei (Baldi, Mersenne, Fabri, Roberval u. a.).^{[Anm. 4]} Explizit findet man diese Definition des Stoßmittelpunktes allerdings erst später, vor allem in der vielbeachteten Abhandlung über den Stoß von Mariotte, und besonders in der Newtonschen Traditionslinie nach Wallis und Taylor.^[5]

Von Beginn an wurde die Abhängigkeit der Lage des Schwingungsmittelpunkts von der Massenverteilung, also von der Gestalt des Körpers, als die eigentliche Schwierigkeit erkannt. Vorrangige Untersuchungsobjekte waren damals neben den zusammengesetzten Pendeln auch symmetrische Körper wie etwa Zylinder, Kegel, Pyramiden, Kugeln und Keile, die zur Vereinfachung in zwei Dimensionen betrachtet wurden: Kegelschnitte, Kreise, Stäbe und Dreiecke. In der Folge gelang es, die Schwingungsmittelpunkte einzelner Körper experimentell und theoretisch exakt zu bestimmen.

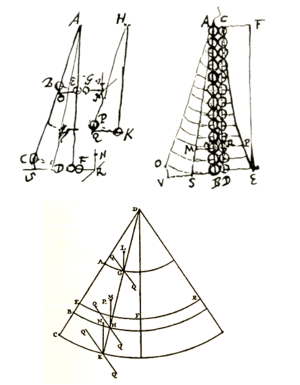
Die erste allgemeine Lösung, den Stoßmittelpunkt beliebig zusammengesetzter Körper theoretisch zu ermitteln, geht auf Christiaan Huygens zurück. Wie schon in der ersten Beweisfassung von 1661 greift er auf damals neuartige Grundlagen zurück, die sich von allen Versuchen über das Hebelprinzip abgrenzen. Insbesondere in der umfassenden Version seines mechanischen Hauptwerkes, dem Horologium Oscillatorium von 1673, bleibt er seinem Beweisverfahren treu.^[6] Es handelt sich um die Deduktion aus den Gesetzen des elastischen Stoßes und einer Erweiterung des nach Torricelli genannten Prinzips der Energieerhaltung des Systemschwerpunktes. Sie kommt einem energetischen Ansatz für mehrere Massenelemente gleich, ohne dass Huygens auf Methoden der Infinitesimalrechnung oder auf den Drallsatz zurückgreifen konnte.

Auf seiner theoretischen Grundlage gelang es Huygens, den Schwingungsmittelpunkt eines aus Stab und Kugel zusammengesetzten Pendelkörpers zu bestimmen, wie er für die technische Konstruktion von Pendeluhren benötigt wird.

Bei aller Anerkennung für seine theoretischen Leistungen auf diesem Gebiet musste Huygens sich zu Lebzeiten auch mit zum Teil polemischer Kritik auseinandersetzen, die ihn persönlich kränkte. So wurde ihm zum Vorwurf gemacht, von unsicheren, nicht-evidenten Prinzipien aus zu beweisen. Daher setzte sich in der Nachfolge Huygens’ der Wettbewerb nach weiteren Beweisverfahren fort, wonach das „dynamisch“ gedachte Hebelprinzip die evidente Grundlage bilden musste. In dieser Folge gelang es zuerst Jakob (‚James‘) Bernoulli 1703, eine Lösung aus dem Hebelprinzip anzugeben, welche den damaligen Anspruch einer gesicherten Grundlage erfüllt.^{[Anm. 5]}

Auch in der Nachfolge von Jakob Bernoullis Lösung galt der Gegenstand des Schwingungsmittelpunktes weiterhin als ein Prüfstein zur Erprobung neuer theoretischer Prinzipien der Mechanik. So wurden einzelne Erweiterungen und Rekonzeptionen vorschlagen:

der Beweis aus den Newtonschen Kraftprinzipien (Brook Taylor und Johann Bernoulli);
der Beweis aus energetischen Prinzipien (Joh. Bernoulli);
die Berücksichtigung von Reibungswiderständen (Jakob Hermann und Joh. Bernoulli);
Beweise aus allgemeineren analytischen Prinzipien der Mechanik (Jean d’Alembert, Leonhard Euler).^[7]

Weder Isaac Newton noch Gottfried W. Leibniz haben sich an den mathematischen Beweisverfahren zum Schwingungsmittelpunkt beteiligt. Letzterer hatte allerdings Huygens brieflich erklärt, dass er dazu auch keinen Anlass sehe, da dessen energetischer Beweis der Sache bereits vollkommen genügen würde.^[7]^:441

Die allgemeine Deduktion des Schwingungsmittelpunkts aus dem Drallsatz geht schließlich auf Leonhard Euler zurück. Sie befindet sich in seinem dritten Mechanikbuch Theoria Motus Corporum Solidorum et Rigidorum von 1765. Darin ergibt sich die Formel ${\mathsf {|OS|={\frac {\theta _{O}}{mr}}}}$ (Notation entsprechend Abb.) bereits als eine gesicherte Folgerung aus den konzeptuellen Grundlagen, die Euler Jahrzehnte zuvor geschaffen hatte: insbesondere aus dem Trägheitsmoment, der Winkelgeschwindigkeit und der nach ihm benannten Momentengleichung.^[8]

Anmerkungen

↑ Man siehe vor allem den Artikel Oscillation von J. d’Alembert und L. Jaucourt, in: Diderot, d’Alembert (Hrsg.), L’Encyclopedie. 1. Auflage. Band 11, Paris 1765, S. 679–680. Und die historische Einleitung in J. L. Lagrange: Mécanique Analytique. 2. Auflage. Nouvelle Édition. Paris 1815. Tome Premier, seconde partie, § I, S. 221 ff.: Sur les différents principes de la Dynamique; Textarchiv – Internet Archive. Anhand der Entwicklung des Schwingungsmittelpunktes von Körpern wird bis heute unter Wissenschaftshistorikern diskutiert, ob die Newtonschen Axiome für die Klassische Mechanik unzureichend sind. Man vergleiche bspw. mit Clifford Truesdell: Die Entwicklung des Drallsatzes. In: Gesellschaft für Angewandte Mathematik und Mechanik (Hrsg.): Zeitschrift für Angewandte Mathematik und Mechanik (= Heft 4/5). Band 44, April 1964, S. 149 – 158, doi:10.1002/zamm.19640440402. Der Stoß- und Schwingungsmittelpunkt von Körpern wird in heutigen Lehrbüchern der (Technischen) Mechanik und Physik im Anwendungskontext eines physikalischen Pendels behandelt. Man vergleiche exemplarisch S. 144 in Herbert Balke: Einführung in die Technische Mechanik. Band 2: Kinetik. Berlin / Heidelberg / New York 2006, ISBN 3-540-26552-X.
↑ Das folgende induktive Herangehen an das Problem des ‚zusammengesetzten Pendels‘ geht auf C. Huygens 1661 zurück (De centro oscillationis). Auf die Weise hat er den Schwingungsmittelpunkt einer Stange (dünner Balken) theoretisch gelöst, nachdem die Richtigkeit bereits von Mersenne experimentell erwiesen war. Zur historischen Version des Beweises, die noch ohne Integralrechnung auskam, siehe IV:141, Seite 141 f. in E.J. Dijksterhuis: Die Mechanisierung des Weltbildes. Berlin, Heidelberg, New York 1956, ISBN 3-540-02003-9.
↑ Man vergleiche auch mit der historischen Einleitung (§1) in M. Malgieri et al.: Two experiments for the measurement of the centre of percussion of a physical pendulum. Eur. J. Phys. 37 (2016), S. 2 (iop.org [abgerufen am 26. Juni 2022]). Gleichbedeutend damit führte Descartes den Erregungsmittelpunkt (centre d‘agitation ) ein: das ist diejenige Stelle, in der sich sämtliche Bewegungsgrößen beim Schlag vereinigen würden. Diese Bezeichnung ist noch in älterer Literatur zu finden, hat sich aber nicht durchgesetzt.
↑ Im Modell eines dynamisch angenommenen Hebels kann nach damaliger Vorstellung nur eine maximale Wirkung erzielt werden, wenn sich ein Momentengleichgewicht während der Drehung zwischen Körperschwerpunkt und dem Zentrum des Impetus einstellt, eine Art Zentrum der trägen Körpermasse und Massengeschwindigkeit. Eine detaillierte Untersuchung im Übergang von der scholastischen Tradition zur neuzeitlichen Mechanik bietet Pierre Duhem, Études sur Léonard de Vinci, ceux qu’il a lus et ceux qui l’ont lu. Paris 1906, ab Kapitel III, Abschn. IV und V, ab S. 108: Le centre de la gravité accidentelle; Textarchiv – Internet Archive.
↑ Bernoullis Beweis enthält konzeptuell bereits den Ansatz des d’Alembertschen Prinzips und ist so auch in die Literatur eingegangen. Man beachte etwa René Dugas, A History of Mechanics. New York (Dover Publ.) 1988, Kap. 4: ab S. 242. books.google.de eingeschränkte Buchvorschau. Die Originalschrift lautet: Jakob Bernoulli, Démonstration générale du centre de Balancement ou d’Oscillation, tirée de la nature du Levier. Mémoires de l’Academie Royale, Paris 1703, S. 78; gallica.bnf.fr

Einzelnachweise

↑ ^a ^b ^c ^d ^e ^f ^g ^h E. F. Autenrieth, Max Ensslin: Technische Mechanik: Ein Lehrbuch der Statik und Dynamik für Ingenieure. 3. Auflage. Springer-Verlag, Berlin 1922, ISBN 3-642-98876-8 (archive.org).
↑ D. Gross, W. Hauger, J. Schröder, W. A. Wall: Technische Mechanik 3. Kinetik. Springer Vieweg Verlag, Heidelberg 2021, ISBN 978-3-662-63064-8, S. 111–181, doi:10.1007/978-3-662-63065-5 (Bewegung eines starren Körpers).
↑ Siehe dazu Baldis Kommentar zu Questio XIX auf S. 131 seiner Schrift In Mechanica Aristotelis Problemata Exercitationes. Mainz 1621. doi:10.3931/e-rara-8255
↑ Marin Mersenne, Tractatus Mechanicus – Theoreticus et Practicus. Paris 1644, S. 83 f.: Proposition 25: Erläuterung verschiedener Gedanken zur Stoßkraft und Aufdeckung von deren Schwierigkeit. Abgedruckt in M. Mersenne: Cogitata Physico Mathematica. Paris 1644. S. 685 ff.; digitale-sammlungen.de
↑ Siehe hierzu Edme Mariotte, Traité de la Percussion ou Chocq du Corps, Paris 1673, S. 281: Proposition XVII: Trouver le centre de Percussion d’un pendule composé, sowie Brook Taylor: Methodus Incrementorum Directa & Inversa. London 1715, S. 100; Prop. XXV.Prob.XX. (PDF; 0,2 MB) 17centurymaths.com, englische Übersetzung mit lateinischem Original hrsg. v. Ian Bruce; abgerufen am 9. September 2022.
↑ Siehe Oeuvres complètes de Christiann Huygens. Hrsg. v. D. de Haan, J. Bosscha, D. Korteweg. Band XVI, ab S. 416; und Band XVIII, ab S. 68. Amsterdam 1967. Textarchiv – Internet Archive De Centro Oscillationis (1661) Horologium Oscillatorium. 17centurymaths.com, englische Übersetzung mit lateinischem Original hrsg. v. Ian Bruce; abgerufen am 9. September 2022.
↑ ^a ^b Christiane Vilain: La Question du ‘Centre d’Oscillation’ de 1660 à 1690. Physis - Rivista Internazionale di Storia Della Scienza, Vol. 37 (2000), S. 21 - 51. C. Vilain: La Question du ‘Centre d’Oscillation’ de 1703 à 1743. Physis (37) 2000, S. 439 - 466 (olschki.it [abgerufen am 10. September 2022]).
↑ Leonhard Euler: Theoria Motus Corporum Solidorum et Rigidorum. Rostock / Greifswald 1765. Caput VII, ab Seite 204 Online abgerufen am 11. April 2022. Neu herausgegeben in: Leonhardi Euleri Opera Omnia, Ser. 2 (Opera Mechanica et Astronomica), Vol. 3. Hrsg. v. Charles Blanc. Bern 1948. (Eneström-Nr. 289). Die zweite Auflage von 1790 ist von Jakob Philipp Wolfers ins Deutsche übersetzt worden: J. Ph. Wolfers (Hrsg.): Leonhard Euler’s Mechanik oder analytische Darstellung der Wissenschaft von der Bewegung – Dritter Teil: Theorie der Bewegung fester oder starrer Körper. Greifswald 1853. Hierin Kapitel VII, ab S. 154: Von der schwingenden Bewegung schwerer Körper; Textarchiv – Internet Archive.

[2] Man siehe vor allem den Artikel Oscillation von J. d’Alembert und L. Jaucourt, in: Diderot, d’Alembert (Hrsg.), L’Encyclopedie. 1. Auflage. Band 11, Paris 1765, S. 679–680. Und die historische Einleitung in J. L. Lagrange: Mécanique Analytique. 2. Auflage. Nouvelle Édition. Paris 1815. Tome Premier, seconde partie, § I, S. 221 ff.: Sur les différents principes de la Dynamique; Textarchiv – Internet Archive. Anhand der Entwicklung des Schwingungsmittelpunktes von Körpern wird bis heute unter Wissenschaftshistorikern diskutiert, ob die Newtonschen Axiome für die Klassische Mechanik unzureichend sind. Man vergleiche bspw. mit Clifford Truesdell: Die Entwicklung des Drallsatzes. In: Gesellschaft für Angewandte Mathematik und Mechanik (Hrsg.): Zeitschrift für Angewandte Mathematik und Mechanik (= Heft 4/5). Band 44, April 1964, S. 149 – 158, doi:10.1002/zamm.19640440402. Der Stoß- und Schwingungsmittelpunkt von Körpern wird in heutigen Lehrbüchern der (Technischen) Mechanik und Physik im Anwendungskontext eines physikalischen Pendels behandelt. Man vergleiche exemplarisch S. 144 in Herbert Balke: Einführung in die Technische Mechanik. Band 2: Kinetik. Berlin / Heidelberg / New York 2006, ISBN 3-540-26552-X.

[4] Das folgende induktive Herangehen an das Problem des ‚zusammengesetzten Pendels‘ geht auf C. Huygens 1661 zurück (De centro oscillationis). Auf die Weise hat er den Schwingungsmittelpunkt einer Stange (dünner Balken) theoretisch gelöst, nachdem die Richtigkeit bereits von Mersenne experimentell erwiesen war. Zur historischen Version des Beweises, die noch ohne Integralrechnung auskam, siehe IV:141, Seite 141 f. in E.J. Dijksterhuis: Die Mechanisierung des Weltbildes. Berlin, Heidelberg, New York 1956, ISBN 3-540-02003-9.

[7] Man vergleiche auch mit der historischen Einleitung (§1) in M. Malgieri et al.: Two experiments for the measurement of the centre of percussion of a physical pendulum. Eur. J. Phys. 37 (2016), S. 2 (iop.org [abgerufen am 26. Juni 2022]). Gleichbedeutend damit führte Descartes den Erregungsmittelpunkt (centre d‘agitation ) ein: das ist diejenige Stelle, in der sich sämtliche Bewegungsgrößen beim Schlag vereinigen würden. Diese Bezeichnung ist noch in älterer Literatur zu finden, hat sich aber nicht durchgesetzt.

[8] Im Modell eines dynamisch angenommenen Hebels kann nach damaliger Vorstellung nur eine maximale Wirkung erzielt werden, wenn sich ein Momentengleichgewicht während der Drehung zwischen Körperschwerpunkt und dem Zentrum des Impetus einstellt, eine Art Zentrum der trägen Körpermasse und Massengeschwindigkeit. Eine detaillierte Untersuchung im Übergang von der scholastischen Tradition zur neuzeitlichen Mechanik bietet Pierre Duhem, Études sur Léonard de Vinci, ceux qu’il a lus et ceux qui l’ont lu. Paris 1906, ab Kapitel III, Abschn. IV und V, ab S. 108: Le centre de la gravité accidentelle; Textarchiv – Internet Archive.

[11] Bernoullis Beweis enthält konzeptuell bereits den Ansatz des d’Alembertschen Prinzips und ist so auch in die Literatur eingegangen. Man beachte etwa René Dugas, A History of Mechanics. New York (Dover Publ.) 1988, Kap. 4: ab S. 242. books.google.de eingeschränkte Buchvorschau. Die Originalschrift lautet: Jakob Bernoulli, Démonstration générale du centre de Balancement ou d’Oscillation, tirée de la nature du Levier. Mémoires de l’Academie Royale, Paris 1703, S. 78; gallica.bnf.fr

[autenrieth-1] ↑ ^a ^b ^c ^d ^e ^f ^g ^h E. F. Autenrieth, Max Ensslin: Technische Mechanik: Ein Lehrbuch der Statik und Dynamik für Ingenieure. 3. Auflage. Springer-Verlag, Berlin 1922, ISBN 3-642-98876-8 (archive.org).

[3] D. Gross, W. Hauger, J. Schröder, W. A. Wall: Technische Mechanik 3. Kinetik. Springer Vieweg Verlag, Heidelberg 2021, ISBN 978-3-662-63064-8, S. 111–181, doi:10.1007/978-3-662-63065-5 (Bewegung eines starren Körpers).

[5] Siehe dazu Baldis Kommentar zu Questio XIX auf S. 131 seiner Schrift In Mechanica Aristotelis Problemata Exercitationes. Mainz 1621. doi:10.3931/e-rara-8255

[6] Marin Mersenne, Tractatus Mechanicus – Theoreticus et Practicus. Paris 1644, S. 83 f.: Proposition 25: Erläuterung verschiedener Gedanken zur Stoßkraft und Aufdeckung von deren Schwierigkeit. Abgedruckt in M. Mersenne: Cogitata Physico Mathematica. Paris 1644. S. 685 ff.; digitale-sammlungen.de

[9] Siehe hierzu Edme Mariotte, Traité de la Percussion ou Chocq du Corps, Paris 1673, S. 281: Proposition XVII: Trouver le centre de Percussion d’un pendule composé, sowie Brook Taylor: Methodus Incrementorum Directa & Inversa. London 1715, S. 100; Prop. XXV.Prob.XX. (PDF; 0,2 MB) 17centurymaths.com, englische Übersetzung mit lateinischem Original hrsg. v. Ian Bruce; abgerufen am 9. September 2022.

[10] Siehe Oeuvres complètes de Christiann Huygens. Hrsg. v. D. de Haan, J. Bosscha, D. Korteweg. Band XVI, ab S. 416; und Band XVIII, ab S. 68. Amsterdam 1967. Textarchiv – Internet Archive De Centro Oscillationis (1661) Horologium Oscillatorium. 17centurymaths.com, englische Übersetzung mit lateinischem Original hrsg. v. Ian Bruce; abgerufen am 9. September 2022.

[vilain-12] Christiane Vilain: La Question du ‘Centre d’Oscillation’ de 1660 à 1690. Physis - Rivista Internazionale di Storia Della Scienza, Vol. 37 (2000), S. 21 - 51. C. Vilain: La Question du ‘Centre d’Oscillation’ de 1703 à 1743. Physis (37) 2000, S. 439 - 466 (olschki.it [abgerufen am 10. September 2022]).

[13] Leonhard Euler: Theoria Motus Corporum Solidorum et Rigidorum. Rostock / Greifswald 1765. Caput VII, ab Seite 204 Online abgerufen am 11. April 2022. Neu herausgegeben in: Leonhardi Euleri Opera Omnia, Ser. 2 (Opera Mechanica et Astronomica), Vol. 3. Hrsg. v. Charles Blanc. Bern 1948. (Eneström-Nr. 289). Die zweite Auflage von 1790 ist von Jakob Philipp Wolfers ins Deutsche übersetzt worden: J. Ph. Wolfers (Hrsg.): Leonhard Euler’s Mechanik oder analytische Darstellung der Wissenschaft von der Bewegung – Dritter Teil: Theorie der Bewegung fester oder starrer Körper. Greifswald 1853. Hierin Kapitel VII, ab S. 154: Von der schwingenden Bewegung schwerer Körper; Textarchiv – Internet Archive.

[1]

[Anm. 1]

[2]

[Anm. 2]

[3]

[4]

[Anm. 3]

[Anm. 4]

[5]

[6]

[Anm. 5]

[7]

[8]

Fahrer / Team für die Suche eingeben:

Fahrer / Team für die Suche eingeben:

Eisspeedway

Stoßmittelpunkt

Inhaltsverzeichnis

Beschreibung

Stoßmittelpunkt

Schwingungsmittelpunkt

Mathematisches Pendel

Beispiele

Entstehungsgeschichte

Anmerkungen

Einzelnachweise