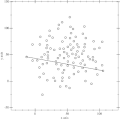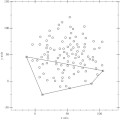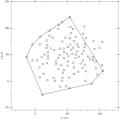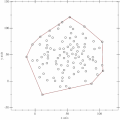
Konvexe Hülle

Die konvexe Hülle einer Teilmenge ist die kleinste konvexe Menge, die die Ausgangsmenge enthält. Betrachtet wird dieses Objekt in unterschiedlichen mathematischen Disziplinen wie zum Beispiel in der konvexen Analysis und der mathematischen Optimierung.
Definitionen
Die konvexe Hülle einer Teilmenge eines reellen oder komplexen Vektorraumes
ist definiert als der Schnitt aller konvexen Obermengen von . Sie ist selbst konvex und damit die kleinste konvexe Menge, die enthält. Die Bildung der konvexen Hülle ist ein Hüllenoperator.
Die konvexe Hülle kann auch beschrieben werden als die Menge aller endlichen Konvexkombinationen:[1]
Der Abschluss der konvexen Hülle ist der Schnitt aller abgeschlossenen Halbräume, die ganz enthalten. Die konvexe Hülle zweier Punkte ist ihre Verbindungsstrecke:
Die konvexe Hülle endlich vieler Punkte ist ein konvexes Polytop.
Eine Menge von Punkten im euklidischen Raum ist konvex, wenn für je zwei beliebige Punkte, die zur Menge gehören, die Menge auch die Verbindungsstrecke enthält. Die konvexe Hülle einer Menge kann wie folgt definiert werden:
- Die minimale konvexe Menge, die als Teilmenge enthält
- Die Schnittmenge aller konvexen Mengen, die als Teilmenge enthalten
- Die Menge aller Konvexkombinationen von Punkten in
- Die Vereinigungsmenge aller Simplexe, deren Eckpunkte in liegen
Es ist nicht offensichtlich, dass die erste Definition sinnvoll ist: Warum sollte es für jedes eine eindeutige minimale konvexe Menge geben, die enthält? Die zweite Definition, die Schnittmenge aller konvexen Mengen, die als Teilmenge enthalten, ist jedoch wohldefiniert. Sie ist eine Teilmenge jeder anderen konvexen Menge , die enthält, weil zu den Schnittmengen gehört. Es ist also genau die eindeutige minimale konvexe Menge, die enthält. Daher sind die ersten zwei Definitionen äquivalent. Jede konvexe Menge, die enthält, muss unter der Annahme, dass sie konvex ist, alle Konvexkombinationen von Punkten in enthalten, so dass die Menge aller Konvexkombinationen in der Schnittmenge aller konvexen Mengen enthalten ist, die enthalten. Umgekehrt ist die Menge aller Konvexkombinationen selbst eine konvexe Menge, die enthält, also enthält sie auch die Schnittmenge aller konvexen Mengen, die enthalten, und daher sind die zweite und dritte Definition äquivalent. Tatsächlich ist nach dem Satz von Carathéodory, wenn eine Teilmenge eines -dimensionalen euklidischen Raums ist, jede Konvexkombination endlich vieler Punkte aus auch eine Konvexkombination von höchstens Punkten in . Die Menge von Konvexkombinationen eines -Tupels von Punkten ist ein Simplex. In der zweidimensionalen Ebene ist es ein Dreieck und im dreidimensionalen Raum ein Tetraeder. Daher gehört jede Konvexkombination von Punkten von zu einem Simplex, dessen Ecken zu gehören, und die dritte und vierte Definition sind äquivalent.
Beispiele

- Das nebenstehende Bild zeigt die konvexe Hülle der Punkte (0,0), (0,1), (1,2), (2,2) und (4,0) in der Ebene. Sie besteht aus dem rot umrandeten Gebiet (inklusive Rand).
- Es gibt eine Klasse von Kurven (darunter z. B. die Bézierkurve), deren Mitglieder die sog. „Convex Hull Property“ (CHP) erfüllen, d. h. ihr Bild verläuft vollständig innerhalb der konvexen Hülle ihrer Kontrollpunkte.
Algorithmen
Die Ermittlung der konvexen Hülle von Punkten im hat als untere Schranke eine asymptotische Laufzeit von ; der Beweis erfolgt durch Reduktion auf das Sortieren von Zahlen. Liegen nur der Punkte auf dem Rand der konvexen Hülle, ist die Schranke bei .
Es bieten sich mehrere Algorithmen zur Berechnung an[2][3]:
- Graham-Scan-Algorithmus mit Laufzeit
- Jarvis-March (2d-Gift-Wrapping-Algorithmus) mit Laufzeit , wobei die Anzahl der Punkte auf dem Rand der Hülle ist
- QuickHull in Anlehnung an Quicksort mit erwarteter Laufzeit ; Worst Case
- Inkrementeller Algorithmus mit Laufzeit
- Chans Algorithmus mit Laufzeit , wobei die Anzahl der Punkte auf dem Rand der Hülle ist.
- Animation des Graham Scan Algorithmus
- Animation des Gift-Wrapping-Algorithmus. Die rote Linien zeigen die bereits gefundenen Strecken der konvexen Hülle, die schwarze zeigt die aktuell Beste, und die grüne Linie zeigt die Strecke, die gerade überprüft wird.
- Animation des QuickHull Algorithmus
Bedeutung für die mathematische Optimierung

Die konvexe Hülle einer zulässigen Menge ist von großer Bedeutung in der mathematischen Optimierung, was am Beispiel der ganzzahligen linearen Optimierung illustriert werden soll.
Etwas Kontext
In der ganzzahligen linearen Optimierung wird innerhalb einer zulässigen Menge nach einem Optimalpunkt mit ganzzahligen Koordinaten gesucht, an welchem die Zielfunktion minimal (oder maximal) ist. Dieses ist, wie in nebenstehender Grafik beispielhaft zu erkennen, durch lineare Ungleichungen und Gleichungen beschrieben, welche alle zulässigen Punkte erfüllen müssen. Dies bedeutet insbesondere, dass nicht alle zulässigen Punkte explizit aufgezählt werden, sondern sich aus der Lösung ganzzahliger linearer Ungleichungen und Gleichungen ergeben. Dies ist die sogenannte Halbraum-Darstellung (engl. half-space representation oder nur h-representation) von Polyedern, in welcher ein Polyeder durch die angrenzenden Halbräume dargestellt wird.[4]
Die Rolle der konvexen Hülle
Das Lösen eines ganzzahligen linearen Optimierungsproblems ist eine NP-schwere Aufgabe, wohingegen in dem kontinuierlichen Gegenstück, also der kontinuierlichen linearen Optimierung Lösungsalgorithmen mit polynomieller Laufzeit (Innere-Punkte-Verfahren) zur Verfügung stehen. Die Ganzzahligkeitsbedingung ist also verantwortlich für die erhöhte Komplexität und könnte umgangen werden, falls statt der obigen Beschreibung der Menge ihre konvexe Hülle effizient berechnet werden könnte, da das lineare ganzzahlige Optimierungsproblem
und das lineare kontinuierliche Optimierungsproblem
dieselben Lösungen besitzen.[5] Dies ist in der Praxis nicht direkt umsetzbar, da die Berechnung der Halbraum-Darstellung von basierend auf der Kenntnis der Menge selbst eine NP-schwere Aufgabe ist, wird aber für die Berechnung von Schnittebenen im Branch-and-Cut-Verfahren der kombinatorischen Optimierung mit großem Erfolg eingesetzt.[6]
Weblinks
- Allgemeines zu konvexen Hüllen samt Algorithmen zur Berechnung
- Zum randomisierten Algorithmus
- Animation des Graham Scan Algorithmus
- Animation des Gift-Wrapping-Algorithmus
- Animation des QuickHull Algorithmus
Einzelnachweise
- ↑ Wolfram MathWorld: Convex Hull
- ↑ Franco P. Preparata, Michael Ian Shamos: Computational Geometry - An Introduction. Springer-Verlag, 1985, 1st edition: ISBN 0-387-96131-3; 2nd printing, corrected and expanded, 1988: ISBN 3-540-96131-3; Russian translation, 1989: ISBN 5-03-001041-6.
- ↑ GitHub, Inc.: Convex Hull Algorithms
- ↑ Günter M. Ziegler: Lectures on polytopes (= Graduate texts in mathematics). Updated seventh printing of the first edition Auflage. Springer, New York, NY 2007, ISBN 978-0-387-94329-9.
- ↑ Laurence A. Wolsey: Integer programming. Second edition Auflage. Wiley, Hoboken, NJ Chichester, West Sussex 2021, ISBN 978-1-119-60653-6.
- ↑ George L. Nemhauser, Laurence A. Wolsey: Integer and combinatorial optimization (= Wiley-Interscience series in discrete mathematics and optimization). Wiley, New York Chichester Weinheim [etc.] 1999, ISBN 978-0-471-35943-2.