Kegelradgetriebe, auch Winkelgetriebe, sind eine Getriebe-Bauform. Sie dienen zum Übertragen von Drehbewegungen und Drehmomenten. Charakteristisches Merkmal sind die winklig zueinander stehenden An- und Abtriebswellen, deren Achsen einen gemeinsamen Schnittpunkt besitzen. Die Kraftübertragung erfolgt durch Kegelräder. Bei Achsversatz (wenn sich die Achsen von Kardanwelle und Antriebswellen nicht schneiden) spricht man auch von Kegelradschraubgetrieben (entspricht Hypoidgetrieben).

Bei Kegelradschraubgetrieben ist der Gleitanteil während der Drehbewegung höher als bei Kegelradwälzgetrieben. Das heißt, die Zähne wälzen und gleiten ab. Das Gleiten kommt durch Relativbewegungen der Berührungsflächen des Kegelrades und Kegelritzels zustande. Diese Wälz- oder Gleitbewegung bei Hypoidkegelradgetrieben begünstigt höhere Übersetzungsverhältnisse und entsprechend bessere Wirkungsgrade beim Anfahren im Vergleich zum Schneckengetriebe.

Ein Kegelradgetriebe besteht aus einem Kegelrad (oft Tellerrad) und aus einem Kegelritzel. Die Achsen sind häufig 90° versetzt, andere Winkel sind möglich. Einsatzgebiete dieser Winkelgetriebe sind dort, wo hohe Untersetzungen, Drehmomente und Bewegungen gefragt sind. Meist erfolgt der Antrieb über das Kegelritzel, linke und rechte Drehrichtungen sind möglich.

Das Übersetzungsverhältnis ist der Quotient der Zähnezahl z2 des Kegelrades durch die Zähnezahl z1 des Kegelritzels. Eine Selbsthemmung wie bei Schneckengetrieben kommt nicht vor. Kegelradgetriebe werden als Leistungsgetriebe in Pressen, Walzwerken, Werkzeugmaschinenbau sowie in der Automation eingesetzt, überall dort, wo Bewegungen und Kräfte winklig übertragen werden.

Das Zahnhöhenprofil aller Kegelradsätze basiert auf einer Oktoide 1. oder 2. Ordnung oder einer Kugelevolvente,^[1] während das Zahnhöhenprofil von Stirnrädern auf einer Evolvente basiert.

Grundformen von Kegelradsätzen mit dem Unterscheidungsmerkmal der Flankenleitlinie sind:

• Geradverzahnungen: Die Flankenlinien der Planradverzahnung sind Geraden, die durch die Planradmitte gehen.
• Schrägverzahnungen: Die Flankenlinien sind Geraden. Sie bilden einen Kreis um die Planradmitte.
• Bogenverzahnungen: Die Flankenlinien bilden Kurven. Die Flankenlinien können beispielsweise Kreisbögen, Evolventen oder Zykloiden sein.^[2] Kreisbogen Circular Arc = Gleason und Kurvex, Epizykloide = Klingelnberg Zyklo-Palloid(R), Evolvente = Klingelnberg Palloid(R)

Das Geradzahnkegelrad als Maschinenelement wird schon um 1780 erwähnt, die ersten Patente wurden um 1876 an William Gleason erteilt. Geradzahnkegelräder haben trotz der Einengung ihres Einsatzbereiches noch ein weites Feld für die Verwendung. Die Grenzen ihres Einsatzes sind die Umfangsgeschwindigkeit, das Geräusch und die übertragbare Leistung. Die Grenze der Umfangsgeschwindigkeit wird allgemein mit 8 m/s genannt. Das Geräusch und die übertragbare Leistung stehen mit dem Überdeckungsgrad in engem Zusammenhang. Anders als bei Spiral- und Hypoidkegelrädern ergibt sich der Überdeckungsgrad bei Geradzahnkegelrädern nur aus dem reinen Profilüberdeckungsgrad. Dieser bewegt sich – je nach Übersetzungsverhältnis – zwischen 1 und 1,7 bei großen Zähnezahlen. Beim ursprünglichen Geradzahnkegelrad war die Längsrichtung des Zahnes geradlinig. Dieser Zahnverlauf hatte zur Folge, dass bei geringsten Abdrängungen der Achsen sich das Zahntragen sofort innen, außen, am Zahnkopf oder -fuß konzentrierte. Dadurch wird das Geräusch wesentlich verstärkt und die Zahnbelastbarkeit stark herabgesetzt.

Durch die geometrische Anordnung der Werkzeuge entsteht der längsballige Zahn. Die Größenordnung der Längsballigkeit kann durch Einsatz von Werkzeugen mit unterschiedlichen Eingriffswinkeln variiert werden. Bei der Auslegung eines Geradzahnkegelradsatzes muss, da es sich um eine abgewälzte Verzahnung handelt, auf das Übersetzungsverhältnis, die Mindest-Zähnezahlen und den Eingriffswinkel Rücksicht genommen werden. Für den möglichen Unterschnitt ist die Mindest-Zähnezahl und der Eingriffswinkel verantwortlich.

Neben den mit Werkzeugmaschinen wie Gleason hergestellten Evolventen als Oktoide 1. und 2. Art gibt es noch die Möglichkeit der Kugelevolvente. Sie kann nur mit Schmiedeverfahren, 5-Achsenmaschinen oder neu mit 3D-Druckern hergestellt werden. Der Vorteil der Kugelevolvente ist bei idealer Fertigung ein Abrollen ohne Schlupf und damit ein erheblich geringerer Verschleiß in den Kontaktflächen der Zähne. Im Schmiedeverfahren können die Parameter wie Eingriffswinkel optimal auf die Anwendung eingestellt werden. Der Zahn muss ohne Hinterschnitt in der Schmiederichtung und damit gut entformbar für geringen Werkzeugverschleiß sein. Ein großer Teil der geradverzahnten Räder und Ritzel in Differentialgetrieben für LKWs und PKWs werden in Deutschland geschmiedet mit Kugelevolvente. Da beim Schmieden mit Warmumformen oder Halbwarmumformen die Stahlstruktur des Rohlings nur umgeformt aber nicht zerstört wird durch ein Schneidwerkzeug, sind diese Radsätze erheblich höher belastbar.

Das Schrägzahnkegelrad wird wie das Geradzahnkegelrad konstruiert und gefertigt mit dem Unterschied, dass die Flankenlinien einen Kreis um die Planradmitte tangieren. Ansonsten hat die oben gemachte Aussage für das Geradzahnkegelrad auch hier Gültigkeit.

Bei Geradzahn-Stirnrädern tritt als Resultierende der Umfangskraft eine Komponente als Radialbelastung auf, die in ihrer resultierenden Lage lediglich durch den Eingriffswinkel bestimmt wird. Neben dieser Radialkraft, die also senkrecht zur Achse wirkt, besteht keine Kraft, die parallel zur Achse, also in Achsrichtung, gerichtet ist. Wenn dieses Geradzahn-Stirnrad einen zusätzlichen Zahnschrägungswinkel erhält und man von einem Schraubenrad oder einem Schrägzahn-Stirnrad spricht, bewirkt dieser Zahnschrägungswinkel neben der Radialkraft noch eine Komponente in Achsrichtung. Werden diese Verhältnisse auf ein Kegelrad übertragen, so resultiert aus dem zu übertragenden Drehmoment eine Komponente in radialer Richtung – also senkrecht zur Achse – und eine Komponente in axialer Richtung. In die Rechnung zur Ermittlung der Radial- und Axialkraft geht der Eingriffswinkel der Verzahnung, die Winkelfunktion des Kegelwinkels und somit das Übersetzungsverhältnis ein. Da die beiden Grund- oder Ausgangswerte für diese Rechnung für beide Drehrichtungen die gleichen sind, bleibt auch die Größe und Richtung dieser Kräfte konstant.

Auch schrägverzahnte und bogenverzahnte Kegelräder können von der im geraden Fall schlupffreien Kugelevolvente profitieren. Der Schlupf durch die Schräge oder den Bogen ist nicht zu verhindern und wird durch die größere Tragfähigkeit der Verzahnung mehr als aufgewogen. Im Schiffsbau werden diese Räder für Strahlantriebe eingesetzt um höheren Belastungen standzuhalten und längere Laufzeiten zu erreichen. Diese Räder sind dann nur mit 5-Achsen-Werkzeugmaschinen zu fertigen.^[3]

Bei den Geradzahnkegelrädern wurde erwähnt, dass der Gesamt-Überdeckungsgrad der Verzahnung im Stirnschnitt lediglich aus dem Profilüberdeckungsgrad besteht. Für das geradverzahnte Kegelrad ist der Stirnschnitt gleich dem Normalschnitt. An dieser Stelle soll nochmals daran erinnert werden, dass das Geräuschverhalten einer Kegelradverzahnung auf die Größe des Überdeckungsgrades bezogen werden kann. Bei Spiralkegelrädern setzt sich der Gesamt-Überdeckungsgrad aus dem Profilüberdeckungsgrad und der Sprungüberdeckung zusammen.^[4] Da mit Vergrößerung des mittleren Spiralwinkels die Sprungüberdeckung zunimmt, lässt sich also durch Änderung des Spiralwinkels bei gleichbleibendem Eingriffswinkel der Gesamt-Überdeckungsgrad wesentlich verändern.

Der Anwendungsbereich von Spiralkegelrädern setzt dort ein, wo Geradzahn-Kegelräder bzw. Schrägzahnkegelräder die gestellten Forderungen nicht mehr erfüllen können. Bei Geradzahnkegelrädern wurden drei Faktoren erwähnt, die den Einsatz dieses Rädertyps begrenzen. Es waren die Umfangsgeschwindigkeit, das Geräusch und die übertragbare Leistung.

Bei der Betrachtung des Geräuschverhaltens bleibt man beim Spiralwinkel, der, wie schon erwähnt, die Größe des Gesamt-Überdeckungsgrades maßgebend beeinflusst. Geräuschuntersuchungen an Stirnrädern haben gezeigt, dass bei einer Erhöhung des Gesamt-Überdeckungsgrades von 1 bis etwa 2,5 ein ständiges Absinken des Geräuschpegels zu verzeichnen war. Interessant ist dabei die Feststellung, dass eine weitere Vergrößerung des Überdeckungsgrades über 2,5 hinaus auf etwa 3 oder 4 keine weitere Geräuschminderung brachte. Mit gewissen Einschränkungen lassen sich die Verhältnisse der Überdeckung auf Kegelräder übertragen.

Auch die übertragbare Leistung ist durch die Veränderung des Gesamt-Überdeckungsgrades beeinflussbar. Bei der Festigkeitsberechnung der Kegelradverzahnung geht die Größe des Überdeckungsgrades in die Rechnung ein. Daraus folgt, dass bei gleichen Radabmessungen und gleichem zu übertragendem Drehmoment durch Veränderung des Spiralwinkels die spezifische Belastung in Bezug auf die Zahnfußbiegespannung reduziert werden kann. Zusammenfassend lässt sich feststellen, dass der Vorteil der Spiralkegelräder gegenüber den Geradzahn- und Schrägzahnkegelrädern durch größere erreichbare Umfangsgeschwindigkeit, besseres Geräuschverhalten und höhere zu übertragende Leistung charakterisiert wird.

Durch die hier aufgeführten Vorteile des Spiralkegelradsatzes wird der Anwendungsbereich solcher Kegelräder naturgemäß sehr groß. Die Antriebsachsen von Automobilen und anderen Fahrzeugen wären bei den heutigen Geschwindigkeiten ohne diese Spiralkegelräder nicht mehr denkbar. Der Werkzeugmaschinenhersteller bedient sich vorwiegend dieses Maschinenelementes, da die Schnittgeschwindigkeiten in der mechanischen Fertigung und somit die Spindeldrehzahlen in den letzten Jahren wesentlich erhöht wurden. Auf dem Sektor der stationären Getriebe, die dem allgemeinen Maschinenbau hinzugerechnet werden, wird überwiegend der Spiralkegelradsatz verwendet.

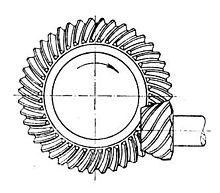
Hypoidkegelräder sind eine Form der Spiralkegelräder. Der grundsätzliche Unterschied besteht darin, dass die Ritzel- und Tellerradachsen nicht in einem Punkt zusammenlaufen, das heißt die Ritzelachse ist gegenüber der Radachse in der Höhe versetzt. Dieser Versatz wird Achsversetzung genannt. Die Achsversetzung sollte für Pkw- und leichte Lkw-Achsgetriebe 40 % und für Lkw, Schlepper, Autobusse und Schienenfahrzeuge einen Grenzwert von 20 % der Außenkegeldistanz nicht überschreiten.

Die Vorteile des Hypoidkegelradsatzes lassen sich wie folgt zusammenstellen: ^[4]

• Durch die Achsversetzung bekommt das Ritzel einen größeren Spiralwinkel als das Tellerrad. Der sich aus dem größeren Spiralwinkel ergebende größere Stirnmodul hat eine Vergrößerung des Teilkreisdurchmessers des Hypoid-Ritzels zur Folge. Daraus ergibt sich eine höhere Belastbarkeit eines Hypoid-Getriebes gegenüber einem Spiralkegelradsatz. Somit reduzieren sich die Flächenpressungen auf den Zähnen.

• Durch die im ersten Punkt erwähnte Vergrößerung des Spiralwinkels des Ritzels wird der Überdeckungsgrad der Verzahnung erhöht. Somit können bei gleichen Dimensionen höhere Übersetzungen realisiert werden als bei Spiralverzahnungen.

• Durch die Achsversetzung kann/muss in den meisten Fällen konstruktiv noch ein zusätzliches Lager für das Ritzel vorgesehen werden. Dadurch werden die Abdrängungswerte als relative Bewegung der Ritzel- und der Tellerradachse zueinander wesentlich verbessert.

Hypoidkegelräder werden neben dem allgemeinen Maschinenbau hauptsächlich in der Automobilindustrie verwendet. Durch die Achsversetzung tritt ein zusätzliches Gleiten der Verzahnung in Zahnlängsrichtung ein. Dieses zusätzliche Längsgleiten ist kein Nachteil, jedoch muss für die Schmierung ein Hochdrucköl verwendet werden.

• Kegelradhobelmaschinen für gerade und schräg verzahnte Kegelradsätze (Fertigbearbeitung nach dem Härten durch Läppen)
• Kegelradfräsmaschinen mit Weich- und Hartbearbeitungsmesserköpfen für Klingelnberg-Zyklo-Palloid-Spiralkegelräder
• Kegelradfräsmaschinen mit sogenannten „Tannenbaum“-Palloid-Fräsern für Klingelnberg-Palloid-Spiralkegelräder (Fertigbearbeitung nach dem Härten durch Läppen)
• Kegelradfräs- und Kegelradschleifmaschinen für Gleason-Circular-Arc-Spiralkegelräder.
• Präzisionsschmieden mit Warm- oder Halbwarmumformen und Kalibrieren bzw. Taumelschmieden für gerade Kegelradsätze mit hohen Stückzahlen.^[5]

Kegelradfräsmaschinen werden nach wie vor in der Serienfertigung erfolgreich eingesetzt. Das 5-Achsen-Fräsen ist für die Serie, bei der in der Regel kleine Moduln und Durchmesser verzahnt werden, aufgrund der hohen Fertigungszeit bei kleinen Zahnlücken nicht wirtschaftlich.

Bei Großkegelrädern und kleinen Stückzahlen wird zwischenzeitlich vermehrt das 5-Achs-Fräsen auf 5-achs-simultanfähigen Bearbeitungszentren mit unprofilierten Standardwerkzeugen in der Weich- und Hartbearbeitung gewählt.

Bei der Herstellmethode „5-Achs-Fräsen“ entfallen die üblicherweise notwendigen Korrekturschleifen bei der Fertigbearbeitung zur Erzielung eines passenden Tragbildes. Durch eine professionelle TCA Zahnkontaktanalyse wird bereits bei Auslegung des Kegelradsatzes durch eine Laufprüfsimulation auf Basis der 3D-Modelle das Tragbild theoretisch „abgerollt“/geprüft und beurteilt. Deckt sich das Tragbild nicht mit den technischen Vorgaben, wird durch Datenänderung in der Auslegung das Tragbild vor Fertigungsbeginn angepasst. Das Tragbild am gefertigten Kegelradsatz entspricht deckungsgleich auf Anhieb dem simulierten Tragbild anhand der Volumenmodelle von Rad und Ritzel. Nachträgliche Anpassarbeiten entfallen in der Regel.

Die verschiedenen Materialien, die für die Herstellung von Kegelrädern verwendet werden, umfassen eine Vielzahl von Gusseisen, NE-Material und nichtmetallischen Materialien.

Die Auswahl des Materials hängt von verschiedenen Faktoren und Betriebsbedingungen ab:

• Art der Leistung
• Umfangsgeschwindigkeit
• Grad der erforderlichen Genauigkeit
• Verfahren zur Herstellung
• gewünschte Größe und Gewicht des Antriebs
• zulässige Spannung
• Stoßfestigkeit
• Verschleißfestigkeit

Folgende Werkstoffe kommen in Frage:

1. Gusseisen besitzt gute Trageigenschaften, lässt sich leicht bearbeiten und in spezielle Formen gießen. Es ist geeignet, wenn große Zahnräder mit komplizierter Form benötigt werden.
2. Stahl ist ausreichend stark und sehr widerstandsfähig gegen Verschleiß durch Abrieb.
3. Stahlguss wird für hohe Belastungen und schwierige Herstellung der Kegelräder verwendet.
4. Vergütungsstähle finden Anwendung für industrielle Getriebe, die eine hohe Zähigkeit bei hoher Festigkeit erfordern.
5. Wärmebehandelte Stähle (wie Einsatz- oder Nitrierstähle) werden dort eingesetzt, wo sehr hohe Zahnfestigkeit und eine sehr geringe Abnutzung der Zähne erforderlich ist.
6. Aluminium wird dort eingesetzt, wo geringe Trägheit der rotierenden Masse nötig ist.
7. Kegelräder aus nichtmetallischen Materialien bewirken geräuscharmen Betrieb bei hohen Umfangsgeschwindigkeiten.

Das Winkelgetriebe hat viele verschiedene Anwendungen wie Lokomotiven, maritime Anwendungen, Automobile, Druckmaschinen, Automation, Maschinenbau, Stahlwerke, Fördertechnik oder Prüfstände. Überall dort, wo Kraft und Bewegung winklig übertragen werden, ein hoher Wirkungsgrad im Zyklenbetrieb notwendig ist, sowie Wartungsarmut gefordert ist.

Beispiele

Kegelräder in Differentialgetrieben, das heißt zwei Achsen drehen sich mit unterschiedlichen Geschwindigkeiten, wie sie bei der Kurvenfahrt eines Fahrzeugs vorkommen. Kegelräder werden als wichtigster Mechanismus für Handbohrmaschinen verwendet. Während der Griff des Bohrers in einer vertikalen Richtung gedreht wird, drehen sich die Kegelräder des Spannfutters horizontal. Die Kegelräder in einer Handbohrmaschine haben den zusätzlichen Vorteil einer Erhöhung der Drehzahl des Spannfutters, was es ermöglicht, eine Reihe von unterschiedlichen Materialien zu bohren.

Spiralkegelräder sind wichtige Komponenten für rotierende Antriebssysteme. Diese Komponenten sind erforderlich, wenn mit hoher Geschwindigkeit, hoher Belastung und für eine große Anzahl von Lastwechseln etwas betrieben werden soll. Das wird beispielsweise angewendet, um die Welle eines horizontalen Gasturbinentriebwerks zum vertikalen Rotor umzuleiten. Auch bei Drehtischen von Werkzeugmaschinen findet das Anwendung.

Hypoidkegelräder findet man sehr häufig in der Robotik und Automation. Auch als Vorstufen bei Roboterarme mit Robotergetrieben. Hypoid-Kegelräder haben häufig einstufig eine hohe Übersetzung und geringes Gewicht.^[4]

Um Reibung und Wärme zu minimieren, sowie den Schutz vor Korrosion zu gewährleisten, werden bei Kegelradgetrieben unterschiedliche Schmierungsarten gewählt:

Fettschmierung

Bei Langsamläufen oder Stellantrieben.

Tauchschmierung

Das Kegelrad läuft im Tauchbad.

Umlaufschmierung

Schmiermittel wird gezielt an das Kegelradpaar herangeführt. Geschmiert wird meist mit synthetischen Ölen, selten mit mineralischen Ölen.^[2]

Bei langsam drehenden Kegelradwälzgetrieben reichen meist Radiallager aus. Bei Kegelradschraubgetrieben (Hypoid) entstehen zusätzlich auch Axialkräfte oder Bewegungen, die mit Axiallagern aufgefangen werden müssen. Die Kegelradpaare sind meist aus gehärtetem Stahl gefertigt. Hohe Belastungen und Verschleißarmut sind erwünscht. Um das Geräuschverhalten zu verbessern und den Verschleiß der Zahnflanken möglichst gering zu halten, muss das Kegelrad über Computerprogramme berechnet, der Traganteil optimiert und das Tragbild eingestellt werden.

Weiterhin muss die Steifigkeit bzw. Durchbiegung der Kegelräder berücksichtigt werden. Die Lagerung (evtl. elastisch und winkelausgleichend) muss den Gegebenheiten angepasst werden.

• Kronenräder bieten eine alternative Möglichkeit, Winkeltriebe zu realisieren
• Zahnrad: Darstellung verschiedener Verzahnungstypen

Commons: Kegelradgetriebe – Sammlung von Bildern, Videos und Audiodateien

1. ↑ Patent EP2484474B1: Ermittlungsverfahren für Geometriedaten eines ersten Kegelrades eines Kegelradgetriebes und Kegelradgetriebe, das ein erstes und ein zweites Kegelrad aufweist. Angemeldet am 7. Februar 2011, veröffentlicht am 3. April 2013, Anmelder: Siemens AG, Erfinder: Florian Dort et al.‌
2. ↑ ^{a b} Gustav Niemann, Hans Winter: Maschinenelemente. Band 3: Schraubrad-, Kegelrad-, Schnecken-, Ketten-, Riemen-, Reibradgetriebe, Kupplungen, Bremsen, Freiläufe. 2., völlig neubearbeitete Auflage, berichtigter Nachdruck. Springer, Berlin 1986, ISBN 3-540-10317-1.
3. ↑ Patent EP2580493B1: Tragfähigkeitsoptimierte Kegelradverzahnung. Angemeldet am 27. Mai 2011, veröffentlicht am 17. Dezember 2014, Anmelder: Schottel GmbH, Technische Universität Dresden, Erfinder: Michael Potts et al.‌
4. ↑ ^{a b c} Hermann J. Stadtfeld: Theorie und Praxis der Spiralkegelräder. Berechnung, Herstellung und Optimierung im Zeitalter computergesteuerter Fabrikation. s. n., Rochester NY 1993.
5. ↑ http://www.maschinenmarkt.vogel.de/taumeln-und-praezisionsschmieden-treten-gegen-die-zerspanung-an-a-337456/index2.html
6. ↑ Berthold Schlecht: Maschinenelemente. Band 2: Getriebe – Verzahnungen – Lagerungen. Pearson Studium, München u. a. 2010, ISBN 978-3-8273-7146-1.

• Jan Klingelnberg (Hrsg.): Kegelräder. Springer, Berlin u. a. 2008, ISBN 978-3-540-71859-8.