Johnson-Körper

Die Johnson-Körper sind eine Klasse geometrischer Körper.

Eigenschaften

Johnson-Körper sind streng konvexe Polyeder, die ausschließlich aus regelmäßigen Vielecken aufgebaut sind, aber weder platonische Körper, archimedische Körper, Prismen noch Antiprismen sind. Gemeinsam mit den catalanischen Körpern ist, dass die Ecken eines Johnson-Körpers nicht identisch sind. Eine Besonderheit unter den Johnson-Körpern ist das Pseudo-Rhombenkuboktaeder (J₃₇), dessen Ecken zwar lokal uniform sind, aber nicht global.

1966 veröffentlichte Norman Johnson eine Liste von 92 derartigen Polyedern; seine Annahme, dass sie vollständig ist,^[1] wurde 1969 von Wictor Salgaller bewiesen.^[2]

Liste

Johnson-Körper werden oft mit $J_{n}$ bezeichnet, wobei $n$ die Nummer des Körpers in der folgenden Liste ist. Beispielsweise ist die Dreieckskuppel $J_{3}$ .

In der folgenden Liste ist $E$ die Anzahl der Ecken, $K$ die Anzahl der Kanten, $F_{n}$ die Anzahl der $n$ -eckigen Flächen und $F:=F_{3}+F_{4}+F_{5}+\ldots$ die Anzahl aller Flächen des jeweiligen Körpers.

Pyramiden, Kuppeln und Rotunden

J_n	Körper	Typ	E	K	F	F₃	F₄	F₅	F₆	F₈	F₁₀	Symmetrie
01	Quadratpyramide	Pyramide	5	8	5	4	1	0	0	0	0	C_4v
02	Fünfeckpyramide	Pyramide	6	10	6	5	0	1	0	0	0	C_5v
03	Dreieckskuppel	Kuppel	9	15	8	4	3	0	1	0	0	C_3v
04	Quadratkuppel		12	20	10	4	5	0	0	1	0	C_4v
05	Fünfeckskuppel		15	25	12	5	5	1	0	0	1	C_5v
06	Fünfecksrotunde, ein in der Mitte geteiltes Ikosidodekaeder	Rotunde	20	35	17	10	0	6	0	0	1	C_5v

Modifizierte Pyramiden

J_n	Name	Typ	E	K	F	F₃	F₄	F₅	Symmetrie
07	verlängerte Dreieckpyramide	verlängerte Pyramide	7	12	7	4	3	0	C_3v
08	verlängerte Quadratpyramide (gleichzeitig erweitertes Hexaeder bzw. Quadratprisma)		9	16	9	4	5	0	C_4v
09	verlängerte Fünfeckpyramide		11	20	11	5	5	1	C_5v
10	verdreht verlängerte Quadratpyramide	verdreht verlängerte Pyramide	9	20	13	12	1	0	C_4v
11	verdreht verlängerte Fünfeckpyramide (beschnittenes Ikosaeder)	verdreht verlängerte Pyramide	11	25	16	15	0	1	C_5v
12	Dreiecksbipyramide	Bipyramide	5	9	6	6	0	0	D_3h
13	Fünfecksbipyramide	Bipyramide	7	15	10	10	0	0	D_5h
14	verlängerte Dreiecksbipyramide	verlängerte Bipyramide	8	15	9	6	3	0	D_3h
15	verlängerte Quadratbipyramide (gleichzeitig zweifach erweitertes Hexaeder bzw. Quadratprisma)		10	20	12	8	4	0	D_4h
16	verlängerte Fünfecksbipyramide		12	25	15	10	5	0	D_5h
17	verdreht verlängerte Quadratbipyramide	verdreht verlängerte Bipyramide	10	24	16	16	0	0	D_4d

Modifizierte Kuppeln und Rotunden

J_n	Körper	Typ	E	K	F	F₃	F₄	F₅	F₆	F₈	F₁₀	Symmetrie
18	verlängerte Dreieckskuppel	verlängerte Kuppel	15	27	14	4	9	0	1	0	0	C_3v
19	verlängerte Quadratkuppel (Beschnittenes kleines Rhombenkuboktaeder)		20	36	18	4	13	0	0	1	0	C_4v
20	verlängerte Fünfeckskuppel		25	45	22	5	15	1	0	0	1	C_5v
21	verlängerte Fünfecksrotunde	verlängerte Rotunde	30	55	27	10	10	6	0	0	1	C_5v
22	verdreht verlängerte Dreieckskuppel	verdreht verlängerte Kuppel	15	33	20	16	3	0	1	0	0	C_3v
23	verdreht verlängerte Quadratkuppel		20	44	26	20	5	0	0	1	0	C_4v
24	verdreht verlängerte Fünfeckskuppel		25	55	32	25	5	1	0	0	1	C_5v
25	verdreht verlängerte Fünfecksrotunde	verdreht verlängerte Rotunde	30	65	37	30	0	6	0	0	1	C_5v
26	verdrehter Doppelkeil	Doppelkuppel	8	14	8	4	4	0	0	0	0	D_2d
27	Dreiecksdoppelkuppel (verdrehtes Kuboktaeder, Disheptaeder)		12	24	14	8	6	0	0	0	0	D_3h
28	Quadratdoppelkuppel		16	32	18	8	10	0	0	0	0	D_4h
29	verdrehte Quadratdoppelkuppel		16	32	18	8	10	0	0	0	0	D_4d
30	Fünfecksdoppelkuppel		20	40	22	10	10	2	0	0	0	D_5h
31	verdrehte Fünfecksdoppelkuppel		20	40	22	10	10	2	0	0	0	D_5d
32	Fünfeckskuppelrotunde	Kuppelrotunde	25	50	27	15	5	7	0	0	0	C_5v
33	verdrehte Fünfeckskuppelrotunde	Kuppelrotunde	25	50	27	15	5	7	0	0	0	C_5v
34	Fünfecksdoppelrotunde (verdrehtes Ikosidodekaeder)	Doppelrotunde	30	60	32	20	0	12	0	0	0	D_5h
35	verlängerte Dreiecksdoppelkuppel	verlängerte Doppelkuppel	18	36	20	8	12	0	0	0	0	D_3h
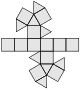
36	verlängerte verdrehte Dreiecksdoppelkuppel		18	36	20	8	12	0	0	0	0	D_3d
37	verlängerte verdrehte Quadratsdoppelkuppel (verdrehtes kleines Rhombenkuboktaeder)		24	48	26	8	18	0	0	0	0	D_4d
38	verlängerte Fünfecksdoppelkuppel		30	60	32	10	20	2	0	0	0	D_5h
39	verlängerte verdrehte Fünfecksdoppelkuppel		30	60	32	10	20	2	0	0	0	D_5d
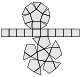
40	verlängerte Fünfeckskuppelrotunde	verlängerte Kuppelrotunde	35	70	37	15	15	7	0	0	0	C_5v
41	verlängerte verdrehte Fünfeckskuppelrotunde	verlängerte Kuppelrotunde	35	70	37	15	15	7	0	0	0	C_5v
42	verlängerte Fünfecksdoppelrotunde	verlängerte Doppelrotunde	40	80	42	20	10	12	0	0	0	D_5h
43	verlängerte verdrehte Fünfecksdoppelrotunde	verlängerte Doppelrotunde	40	80	42	20	10	12	0	0	0	D_5d
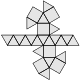
44	verdreht verlängerte Dreiecksdoppelkuppel	verdreht verlängerte Doppelkuppel	18	42	26	20	6	0	0	0	0	D₃
45	verdreht verlängerte Quadratdoppelkuppel		24	56	34	24	10	0	0	0	0	D₄
46	verdreht verlängerte Fünfecksdoppelkuppel		30	70	42	30	10	2	0	0	0	D₅
47	verdreht verlängerte Fünfeckskuppelrotunde	verdreht verlängerte Kuppelrotunde	35	80	47	35	5	7	0	0	0	C₅
48	verdreht verlängerte Fünfecksdoppelrotunde	verdreht verlängerte Doppelrotunde	40	90	52	40	0	12	0	0	0	D₅

Erweiterte Prismen

J_n	Körper	E	K	F	F₃	F₄	F₅	F₆	Symmetrie
49	erweitertes Dreiecksprisma	7	13	8	6	2	0	0	C_2v
50	doppelt erweitertes Dreiecksprisma	8	17	11	10	1	0	0	C_2v
51	dreifach erweitertes Dreiecksprisma	9	21	14	14	0	0	0	D_3h
52	erweitertes Fünfecksprisma	11	19	10	4	4	2	0	C_2v
53	doppelt erweitertes Fünfecksprisma	12	23	13	8	3	2	0	C_2v
54	erweitertes Sechsecksprisma	13	22	11	4	5	0	2	C_2v
55	doppelt erweitertes Sechsecksprisma (para)	14	26	14	8	4	0	2	D_2h
56	doppelt erweitertes Sechsecksprisma (meta)	14	26	14	8	4	0	2	C_2v
57	dreifach erweitertes Sechsecksprisma	15	30	17	12	3	0	2	D_3h

Modifizierte platonische Körper

J_n	Körper	Typ	E	K	F	F₃	F₅	Symmetrie
58	erweitertes Dodekaeder	erweitertes Dodekaeder	21	35	16	5	11	C_5v
59	doppelt erweitertes Dodekaeder (para)		22	40	20	10	10	D_5d
60	doppelt erweitertes Dodekaeder (meta)		22	40	20	10	10	C_2v
61	dreifach erweitertes Dodekaeder		23	45	24	15	9	C_3v
62	doppelt beschnittenes Ikosaeder (meta)	beschnittenes Ikosaeder	10	20	12	10	2	C_2v
63	dreifach beschnittenes Ikosaeder	beschnittenes Ikosaeder	9	15	8	5	3	C_3v
64	erweitertes dreifach beschnittenes Ikosaeder	-	10	18	10	7	3	C_3v

Modifizierte archimedische Körper

J_n	Körper	Typ	E	K	F	F₃	F₄	F₅	F₆	F₈	F₁₀	Symmetrie
65	erweitertes abgestumpftes Tetraeder	erweitertes abgestumpftes Tetraeder	15	27	14	8	3	0	3	0	0	C_3v
66	erweitertes abgestumpftes Hexaeder	erweitertes abgestumpftes Hexaeder	28	48	22	12	5	0	0	5	0	C_4v
67	doppelt erweitertes abgestumpftes Hexaeder	erweitertes abgestumpftes Hexaeder	32	60	30	16	10	0	0	4	0	D_4h
68	erweitertes abgestumpftes Dodekaeder	erweitertes abgestumpftes Dodekaeder	65	105	42	25	5	1	0	0	11	C_5v
69	doppelt erweitertes abgestumpftes Dodekaeder (para)		70	120	52	30	10	2	0	0	10	D_5d
70	doppelt erweitertes abgestumpftes Dodekaeder (meta)		70	120	52	30	10	2	0	0	10	C_2v
71	dreifach erweitertes abgestumpftes Dodekaeder		75	135	62	35	15	3	0	0	9	C_3v
72	verdrehtes Rhombenikosidodekaeder	verdrehtes kleines Rhombenikosidodekaeder	60	120	62	20	30	12	0	0	0	C_5v
73	doppelt verdrehtes kleines Rhombenikosidodekaeder (para)		60	120	62	20	30	12	0	0	0	D_5d
74	doppelt verdrehtes kleines Rhombenikosidodekaeder (meta)		60	120	62	20	30	12	0	0	0	C_2v
75	dreifach verdrehtes kleines Rhombenikosidodekaeder		60	120	62	20	30	12	0	0	0	C_3v
76	beschnittenes kleines Rhombenikosidodekaeder	beschnittenes kleines Rhombenikosidodekaeder	55	105	52	15	25	11	0	0	1	C_5v
77	verdrehtes beschnittenes kleines Rhombenikosidodekaeder (para)	verdrehtes beschnittenes kleines Rhombenikosidodekaeder	55	105	52	15	25	11	0	0	1	C_5v
78	verdrehtes beschnittenes kleines Rhombenikosidodekaeder (meta)		55	105	52	15	25	11	0	0	1	C_s
79	doppelt verdrehtes beschnittenes kleines Rhombenikosidodekaeder		55	105	52	15	25	11	0	0	1	C_s
80	doppelt beschnittenes kleines Rhombenikosidodekaeder (para)	beschnittenes kleines Rhombenikosidodekaeder	50	90	42	10	20	10	0	0	2	D_5d
81	doppelt beschnittenes kleines Rhombenikosidodekaeder (meta)	beschnittenes kleines Rhombenikosidodekaeder	50	90	42	10	20	10	0	0	2	C_2v
82	verdrehtes doppelt beschnittenes kleines Rhombenikosidodekaeder	verdrehtes beschnittenes kleines Rhombenikosidodekaeder	50	90	42	10	20	10	0	0	2	C_2v
83	dreifach beschnittenes kleines Rhombenikosidodekaeder	beschnittenes kleines Rhombenikosidodekaeder	45	75	32	5	15	9	0	0	3	C_3v

Übrige

J_n	Körper	E	K	F	F₃	F₄	F₅	F₆	Symmetrie
84	Trigondodekaeder	8	18	12	12	0	0	0	D_2d
85	abgeschrägtes Quadratantiprisma	16	40	26	24	2	0	0	D_4d
86	Sphenocorona	10	22	14	12	2	0	0	C_2v
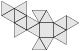
87	erweiterte Sphenocorona	11	26	17	16	1	0	0	C_s
88	Sphenomegacorona	12	28	18	16	2	0	0	C_2v
89	Hebesphenomegacorona	14	33	21	18	3	0	0	C_2v
90	Disphenocingulum	16	38	24	20	4	0	0	D_2d
91	Bilunadoppelrotunde	14	26	14	8	2	4	0	D_2h
92	Dreieckshebesphenorotunde	18	36	20	13	3	3	1	C_3v

Weblinks

Commons: Johnson solids – Sammlung von Bildern, Videos und Audiodateien

Eric W. Weisstein: Johnson Solid. In: MathWorld (englisch).
Johnson Solid (mit diversen Grafiken, englisch, archiviert)

Einzelnachweise

↑ Norman W. Johnson: Convex Solids with Regular Faces. In: Canadian Journal of Mathematics. Band 18, 1966, ISSN 0008-414X, S. 169–200.
↑ Viktor A. Zalgaller: Convex Polyhedra with Regular Faces (= Seminars in Mathematics. Bd. 2, ISSN 0080-8873). Consultants Bureauvon, New York NY 1969.

[1] Norman W. Johnson: Convex Solids with Regular Faces. In: Canadian Journal of Mathematics. Band 18, 1966, ISSN 0008-414X, S. 169–200.

[2] Viktor A. Zalgaller: Convex Polyhedra with Regular Faces (= Seminars in Mathematics. Bd. 2, ISSN 0080-8873). Consultants Bureauvon, New York NY 1969.

[1]

[2]

Fahrer / Team für die Suche eingeben: