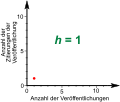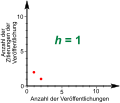h-Index


Der h-Index ist eine Kennzahl für die weltweite Wahrnehmung eines Wissenschaftlers in Fachkreisen. Die Kennzahl basiert auf bibliometrischen Analysen von Zitationen der Publikationen des Wissenschaftlers. Ein hoher h-Index ergibt sich, wenn eine erhebliche Anzahl von Publikationen des Wissenschaftlers häufig in anderen Veröffentlichungen zitiert wird. Der 2005 von dem Physiker Jorge E. Hirsch vorgeschlagene Bewertungsindex wird gelegentlich auch als Hirsch-Index, Hirschfaktor, Hirsch-Koeffizient oder h-number bezeichnet.
Der h-Index eines Wissenschaftlers kann im Laufe der Zeit nicht sinken; andererseits kann er auch nicht allein über die Anzahl seiner Veröffentlichungen steigen.
Der h-Index kann auch posthum steigen. Nach oben begrenzt ist er mit der Anzahl der Publikationen eines Autors.
Definition
Der h-Index eines Wissenschaftlers wurde definiert als die größte Zahl , für die gilt: Publikationen dieses Wissenschaftlers wurden mindestens -mal zitiert.[1]
Äquivalent dazu ist die folgende Definition: Ein Wissenschaftler hat einen Hirsch-Index , wenn von seinen insgesamt Publikationen mindestens -mal und die restlichen Publikationen höchstens -mal zitiert wurden.
Zur Ermittlung kann man alle Veröffentlichungen des Autors nach Zitierhäufigkeiten absteigend aufreihen und so weit durchzählen, bis die -te Veröffentlichung weniger als Zitierungen hat; dann ist .
Laut Hirsch ist ein h-Index von 20 nach 20 Jahren Forschungsaktivität das Zeichen eines erfolgreichen Wissenschaftlers. Ein h-Index von 40 nach 20 Jahren Forschungsaktivität zeige den außergewöhnlichen Wissenschaftler an, der wahrscheinlich nur in Top-Universitäten und großen Forschungslabors gefunden werden könne. Einen h-Index von 60 und höher nach 20 Jahren Forschungsaktivität weisen laut Hirsch nur einzigartige Persönlichkeiten auf.[1]
Beispiele zur Berechnung
Einige Beispiele von Autoren mit jeweils 10 Veröffentlichungen:
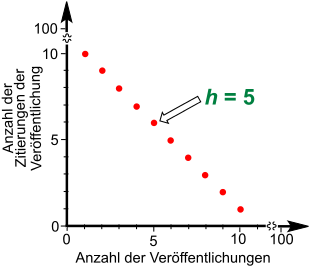
- Bei Zitathäufigkeiten 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 ist der Hirschfaktor 5, weil fünf Veröffentlichungen mindestens fünfmal, die restlichen höchstens fünfmal zitiert wurden. Die sechste Veröffentlichung wurde ebenfalls fünfmal zitiert, sie kann aber nicht mitgezählt werden, weil der Hirschfaktor damit auf 6 steigen würde, und fünf Zitierungen somit nicht mehr ausreichen würden.
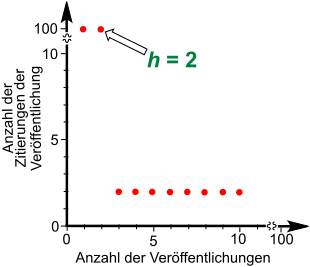
- Bei Zitathäufigkeiten 100, 100, 2, 2, 2, 2, 2, 2, 2, 2 ist der Hirschfaktor 2, weil zwei Veröffentlichungen mindestens zweimal, die restlichen höchstens zweimal zitiert wurden.
- Bei Zitathäufigkeiten 100, 100, 9, 8, 3, 2, 2, 1, 1, 0 ist der Hirschfaktor 4, weil vier Veröffentlichungen mindestens viermal, die restlichen höchstens viermal zitiert wurden.
Beispiel mit zeitlichem Verlauf
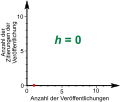
- Bei Veröffentlichung der ersten Arbeit ist diese noch nicht zitiert. Der Autor hat den Hirschfaktor 0.
- Die Arbeit wird irgendwann erstmals zitiert. Der Autor hat den Hirschfaktor 1.
- Der Autor wird noch einmal zitiert. Er behält den Hirschfaktor 1.
- Der Autor schreibt einen neuen Artikel. Er behält den Hirschfaktor 1.
- Auch der zweite Artikel wird einmal zitiert. Er behält den Hirschfaktor 1.
- Nach einiger Zeit sind alle Artikel genau zweimal zitiert. Er erhält den Hirschfaktor 2.
- Die nächsten fünf Artikel erscheinen, ohne zitiert zu werden. Er behält den Hirschfaktor 2.
- Als alle Arbeiten zweimal zitiert sind, bleibt der Hirschfaktor bei 2.
- Der Autor hat mittlerweile zwei Arbeiten, die jeweils zehnmal zitiert sind, und fünf weitere, die nur zweimal zitiert sind. Hirschfaktor 2.
- Eine neue bahnbrechende Arbeit erscheint und wird gleich nach Veröffentlichung zweimal zitiert. Der Autor behält den Hirschfaktor 2.
- Als diese dritte Arbeit ein drittes Mal zitiert wird, erhöht sich der Hirschfaktor auf 3.
- Der Autor hat mittlerweile drei Arbeiten, die jeweils elfmal zitiert sind, und fünf weitere, die dreimal zitiert sind. Hirschfaktor 3.
- Der Autor schreibt weitere drei Artikel, die jedoch nirgends zitiert werden. Der Hirschfaktor bleibt bei 3.
- Ein bisher nur dreimal zitierter Artikel wird ein viertes Mal zitiert. Der Hirschfaktor steigt auf 4.
Hintergründe
Der h-Index zur Bewertung wissenschaftlicher Leistungen wurde 2005 von dem argentinischen Physiker Jorge E. Hirsch in den Proceedings of the National Academy of Sciences vorgeschlagen.[1]
Als Datengrundlage zur Berechnung des bibliometrischen Indikators sind diverse Datenquellen denkbar, die Zitierungen nachweisen. Hirsch selbst schlug vor, maßgeblich die Daten des Web of Science zu benutzen, da diese seinerzeit die verlässlichste und umfassendste Datengrundlage darstellten.
Inzwischen kann der h-Index in vielen Zitationsdatenbanken ermittelt werden, z. B. in Google Scholar, wenn der Autor ein Profil hat.
Beispiel mit unterschiedlichen Datenbasen
Am Beispiel des theoretischen Physikers Stephen W. Hawking (1942–2018) lässt sich der Einfluss der für die Ermittlung des h-Indexes verwendeten Datenbasis gut veranschaulichen. Die Erhebung der Daten erfolgte am 15. Juni 2017:
| Datenbank | Zahl der erfassten Veröffentlichungen |
Gesamtzahl der Zitierungen |
h-Index |
|---|---|---|---|
| Google Scholar | 908 | 121.425 | 118 |
| Scopus | 148 | 29.985 | 66 |
| Web of Science CC | 179 | 37.484 | 78 |
Entwicklung
Der h-Index wird nicht nur als Kennzahl für Autoren verwendet, sondern auch für Institutionen, Arbeitsgruppen, Länder oder Zeitschriften. Für bestimmte Zwecke werden auch Varianten genutzt (s. u.).
Eigenschaften
Der h-Index hat einige Vorteile gegenüber anderen Kennzahlen (wie zum Beispiel der Gesamtanzahl von Zitationen eines Autors oder dem Impact-Faktor), da die Zitationen einer einzigen, viel-zitierten Veröffentlichung keinen großen Einfluss auf den Index haben. Dies kann aber auch als Nachteil interpretiert werden, da eventuell bahnbrechende Artikel nicht entsprechend gewürdigt werden (es kommt quasi zu einer harmonischen Angleichung der Bewertung der Zitate). Außerdem wird weder die Zahl der Koautoren noch die Tatsache berücksichtigt, ob die zitierte Publikation eine Originalarbeit oder ein Übersichtsartikel ist. Generell ist zu beachten, dass durch Zitationen die (unterschiedlich begründete) „Popularität“ und nicht notwendigerweise die wissenschaftliche Relevanz einer Publikation gemessen wird; so hätte der früh verstorbene Évariste Galois trotz seiner grundlegenden Arbeiten für die Mathematik nur einen h-index von 2, und Albert Einstein hätte nach dem Annus Mirabilis einen h-index von 4 gehabt.
Grundsätzlich haben junge Forscher niedrigere h-Indizes als ältere im gleichen Fach, da sie noch weniger publiziert haben. In Fächern, in denen weniger publiziert und zitiert wird, sind die h-Indizes niedriger als in Fächern mit hohem Output. Obwohl eine hohe Produktivität nicht zwangsläufig mit einem höheren Index belohnt wird, so kann der h-Index maximal so hoch wie die Anzahl an Veröffentlichungen sein.
Probleme
Die Erhebung der Grunddaten stellt eine große Schwierigkeit dar. Mit der von Hirsch vorgeschlagenen Datengrundlage (Web of Science von Clarivate) werden unter anderem Buchpublikationen schlecht erfasst, was die Ergebnisse der Erhebung stark beeinflusst. Insbesondere in den Sozial- und Geisteswissenschaften können weitere Veröffentlichungen wie z. B. Buchrezensionen bedeutend sein, ohne dass diese häufig zitiert und damit im h-Index berücksichtigt werden. Wird die Erhebung hingegen auf eine nicht kontrollierte, größere Datengrundlage wissenschaftlicher Veröffentlichungen erweitert (z. B. Google Scholar), so kann der h-Index durch viele Selbstreferenzierungen gezielt manipuliert und leicht in die Höhe getrieben werden, wie 2011 an der Universität Grenoble demonstriert wurde.[2] Deshalb sind h-Indizes immer mit der zugrundeliegenden Datenbank und dem Erhebungsdatum anzugeben. Ferner ist die Abgrenzung von Autoren mit gleichen Namen ein Problem.[3] Durch Verwendung von Identifikatoren wie ORCID wird eine korrekte Zuordnung erreicht.
Die Bedeutung, die der h-Index und vergleichbare bibliometrische Maße für die Karriere von Wissenschaftlern haben, führt zu Optimierungsstrategien, die sich negativ auf die wissenschaftliche Kultur auswirken. So kann es etwa zielführend sein, eine Veröffentlichung in mehrere Teile zu zerlegen und einzeln zu publizieren, eigennutzenorientiert mit Selbstzitaten. Eine weitere mögliche Strategie besteht darin, Gruppen („Denkschulen“) von 10 bis 15 Wissenschaftlern zu bilden, die eine eigene Zeitschrift oder ein ähnliches Publikationsorgan gründen und sich darin gegenseitig häufig zitieren. Ebenso sind Zitationszirkel (auch als Zitierkartelle bezeichnet) eine Möglichkeit, um den persönlichen Faktor besserzustellen. Dabei schließen sich Gruppen von Wissenschaftlern zusammen, die sich gegenseitig bei Veröffentlichung zitieren oder die Gruppenmitglieder bei (absehbar zitierfähigen) Veröffentlichungen als Co-Autoren berücksichtigen. Diese Praktiken können die Seriosität der Wissenschaft untergraben.[4] Entsprechend gibt es Stimmen, den h-Index aufzulösen[5] oder die zahlreichen Defizite des h-Index durch Änderungen zu beheben.[6][7][8][9][10][11]
Wissenschaftler mit hohen h-Indizes
Wissenschaftler mit den höchsten h-Indizes nach Hirsch
Zur Zeit der Publikation des Hirsch-Indexes hatte Edward Witten mit 120 den höchsten h-Index unter Physikern. Andere bekannte Physiker erreichten einen h-Index von 62 bis 107. Für Forscher in Biologie und Biomedizin errechnete Hirsch anhand der Zitierungen in den Jahren von 1983 bis 2002 ebenfalls einen h-Index. Den höchsten h-Index dieser Fachgruppe aus dieser Zeit besaß Solomon H. Snyder mit 191, die folgenden 9 Forscher der Rangfolge hatten h-Indizes von 160 bis 120.[1]
Beispiele für h-Indizes 2021
Die folgenden Beispiele geben den Stand am 7. Mai 2021 laut der Datenbank Scopus wieder.
| Name | Fachgebiet | Veröffent- lichungen |
Summe der Zitierungen |
h-Index | Quelle |
|---|---|---|---|---|---|
| Albert Einstein | Physik | 102 | 25.984 | 41 | [12] |
| Stephen Hawking | Physik | 161 | 44.981 | 75 | [13] |
| Didier Queloz | Physik | 494 | 29.739 | 88 | [14] |
| Christian Drosten | Virologie | 437 | 42.835 | 88 | [15] |
| John B. Goodenough | Chemie | 987 | 130.937 | 164 (27.06.2023) |
[16] |
| Edward Witten | Physik | 303 | 111.651 | 145 | [17] |
| Anthony Fauci | Immunologie | 1180 | 118.166 | 178 | [18] |
| David Baltimore | Virologie | 742 | 125.839 | 179 | [19] |
| Ronald M. Evans | Molekularbiologie | 562 | 136.032 | 180 | [20] |
| Carlo Maria Croce | Krebsforschung | 1298 | 172.299 | 194 | [21] |
| Matthias Mann | Physik | 786 | 168.025 | 204 | [22] |
| Solomon H. Snyder | Neurowissenschaften | 1278 | 180.055 | 218 | [23] |
| George Whitesides | Chemie | 1370 | 241.022 | 228 | [24] |
| Robert Langer | Chemieingenieurwesen | 1761 | 217.459 | 229 | [25] |
| Bert Vogelstein | Krebsforschung | 625 | 296.736 | 238 | [26] |
| Michael Grätzel | Chemie | 1651 | 333.566 | 259 | [27] |
Literatur
- J. E. Hirsch: An index to quantify an individual’s scientific research output. In: Proceedings of the National Academy of Sciences. Band 102, Nummer 46, November 2005, ISSN 0027-8424, S. 16569–16572, doi:10.1073/pnas.0507655102, PMID 16275915, PMC 1283832 (freier Volltext), arxiv:physics/0508025.
- J. E. Hirsch: An index to quantify an individual’s scientific research output that takes into account the effect of multiple coauthorship. In: Scientometrics. 85, 2010, S. 741–754, doi:10.1007/s11192-010-0193-9. (auch arxiv:0911.3144).
- M. Richter: Was misst der h-Index (nicht)? – Kritische Überlegungen zu einer populären Kennzahl für Forschungsleistungen. In: WiSt – Wirtschaftswissenschaftliches Studium. Band 47, Nummer 12, Dezember 2018, S. 64–68.
- A. Sidiropoulos, D. Katsaros, Y. Manolopoulos: Generalized h-index for Disclosing Latent Facts in Citation Networks. In: arXiv. 2006, arxiv:cs/0607066.
- P. Ball: Achievement index climbs the ranks. In: Nature. Band 448, Nummer 7155, August 2007, ISSN 1476-4687, S. 737, doi:10.1038/448737a, PMID 17700666.
Weblinks
- Harzing.com – Publish or Perish Auf Google-Scholar-Daten basierendes kostenloses Analysetool zur Ermittlung des Hirsch-Faktors
- ISI Web of Knowledge – Datenbank die H-Index Auswertung beinhaltet (Zugang nur nach Anmeldung oder über z. B. Campus-Logins)
- SCImagojr.com – H-Index für Zeitschriften (nicht auf Personenebene)
- Der h-Index – Berechnung und Bedeutung der bibliometrischen Kennzahl, Video-Tutorial (deutsch)
Einzelnachweise
- ↑ a b c d J. E. Hirsch: An index to quantify an individual’s scientific research output. In: Proceedings of the National Academy of Sciences. Band 102, Nummer 46, November 2005, ISSN 0027-8424, S. 16569–16572, doi:10.1073/pnas.0507655102, PMID 16275915, PMC 1283832 (freier Volltext), arxiv:physics/0508025.
- ↑ Falsche Forscheridentität – Kennen Sie Ike Antkare? taz.de, 3. März 2011.
- ↑ Der Hirsch-Index ( vom 23. September 2015 im Internet Archive) (PDF-Datei; 23 kB).
- ↑ Interview mit Prof. Dr. Ludwig Winnacker: Für einen Artikel in Science tut man alles. Archiviert vom am 9. Januar 2019; abgerufen am 6. Januar 2019.
- ↑ Rowlands I: Is it time to bury the h-index? 28. März 2018, abgerufen am 9. Januar 2019.
- ↑ Batista P. D., Mônica G. Campiteli, Osame Kinouchi: Is it possible to compare researchers with different scientific interests? In: Scientometrics. 68. Jahrgang, Nr. 1, 2006, S. 179–189, doi:10.1007/s11192-006-0090-4.
- ↑ Antonis Sidiropoulos, Katsaros, Dimitrios and Manolopoulos, Yannis: Generalized Hirsch h-index for disclosing latent facts in citation networks. In: Scientometrics. 72. Jahrgang, Nr. 2, 2007, S. 253–280, doi:10.1007/s11192-007-1722-z.
- ↑ Jayant S. Vaidya: V-index: A fairer index to quantify an individual's research output capacity. In: BMJ. 331. Jahrgang, Nr. 7528, Dezember 2005, S. 1339–c–1340–c, doi:10.1136/bmj.331.7528.1339-c (bmj.com).
- ↑ D. Katsaros, A. Sidiropoulos, Y. Manolopous: Age Decaying H-Index for Social Network of Citations. In: Proceedings of Workshop on Social Aspects of the Web Poznan, Poland, April 27, 2007. 2007.
- ↑ T.R. Anderson, R.K.S Hankin, P.D. Killworth,: Beyond the Durfee square: Enhancing the h-index to score total publication output. In: Scientometrics. 76. Jahrgang, Nr. 3, 2008, S. 577–588, doi:10.1007/s11192-007-2071-2.
- ↑ C. Baldock, Colin G. Orton, Ma, R.M.S and Orton, C.G.: The h index is the best measure of a scientist's research productivity. In: Medical Physics. 36. Jahrgang, Nr. 4, 2009, S. 1043–1045, doi:10.1118/1.3089421, PMID 19472608, bibcode:2009MedPh..36.1043B.
- ↑ Einstein, Albert. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Hawking, Stephen. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Queloz, Didier. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 22. Mai 2021 (englisch).
- ↑ Drosten, Christian. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Goodenough, John B. In: Scopus – Author details. Elsevier B.V., abgerufen am 27. Juni 2023 (englisch).
- ↑ Witten, Edward. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Faucì, Anthony S. In: scopus.com. Scopus, abgerufen am 7. Mai 2021 (englisch).
- ↑ Baltimore, David. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Evans, Ronald M. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Croce, Carlo Maria. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Mann, Matthias. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Snyder, Solomon H. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Whitesides, G. M. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Langer, Robert Samuel M. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Vogelstein, Bert. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).
- ↑ Grätzel, M. In: Scopus preview – Scopus – Author details. Elsevier B.V., abgerufen am 7. Mai 2021 (englisch).