In ökonomischen und ökonometrischen Modellen bezeichnet eine exogene Variable einen veränderlichen Einflussfaktor, der außerhalb des Modells bestimmt wird und bei der systematischen Analyse zum Input eines Modells gehört. Anders ausgedrückt: Exogene Variablen sind in dem Augenblick, in dem sie in das Modell eingebracht werden, fest vorgegeben. Dagegen werden die endogenen Variablen innerhalb des Modells determiniert und stellen somit den Output eines Modells dar. Das mit den Variablen spezifizierte Modell zeigt auf, wie sich die Veränderung einer exogenen Variable ceteris paribus auf alle endogenen Variablen auswirkt.

Im Allgemeinen werden auch erklärende Variablen, die nicht mit der Störgröße einer Regressionsfunktion korreliert sind, als exogene Variablen bezeichnet.^[1]

In Eingleichungsmodellen stimmen die Begriffe erklärte Variable, Regressand und endogene Variable einerseits sowie erklärende Variable, Regressor und exogene Variable andererseits überein. Dagegen können in Mehrgleichungsmodellen endogene Variablen sowohl Regressor, als auch Regressand sein; exogene Variablen jedoch wiederum nur Regressoren.

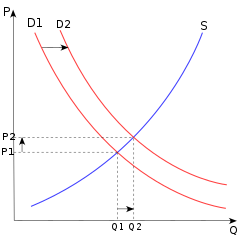
Wenn ein Ökonom herausfinden möchte, wodurch der Preis und die verkaufte Menge von Fahrrädern bestimmt wird, dann stellt er ein ökonomisches Modell auf. Dieses Modell sollte das Verhalten des Fahrradanbieters, des Fahrradnachfragers und die Interdependenzen am Markt beschreiben. Der Ökonom könnte beispielsweise ein Modell aufstellen, bei dem die Nachgefragte Quantität bzw. Menge an Fahrrädern vom Fahrradpreis und vom verfügbaren Einkommen der Nachfrager abhängt: . Hierbei bezeichnet die Nachfragefunktion. Im Folgenden könnte er das Modell dahin spezifizieren, dass das Fahrradangebot der Fahrradläden vom Fahrradpreis und auch von den Preisen der Fahrradeinzelteile (Dynamo, Reflektoren etc.) abhängt: . Hierbei stellt die Angebotsfunktion dar. Des Weiteren wird angenommen, dass sich der Fahrradmarkt im Gleichgewicht befindet: . Das Fahrradmarktmodell beinhaltet zwei exogene Variablen (Preis der Fahrradeinzelteile und verfügbares Einkommen der Nachfrager ) und zwei endogene Variablen (Fahrradpreis und die gehandelte Fahrradmenge ). Durch das Modell sollen die endogenen Variablen erklärt werden. Dagegen sollen die exogenen Variablen nicht erklärt werden: Man nimmt sie als gegeben an. Dieses Modell kann aufzeigen, wie die Veränderung einer der beiden exogenen Variablen (ceteris paribus) die beiden endogenen Variablen beeinflusst. Wenn man annimmt, dass das verfügbare Einkommen der Nachfrager steigt, dann nimmt die Fahrradnachfrage zu. Gleichzeitig steigt auch der Gleichgewichtspreis und die Gleichgewichtsmenge. Analog: Wenn die Preise der Fahrradeinzelteile steigen, dann nimmt das Fahrradangebot ab und der Gleichgewichtspreis und die Gleichgewichtsmenge sinken.^[2]

In der Regressionsanalyse und Ökonometrie ist eine exogene erklärende Variable eine erklärende Variable, die mit der Störgröße unkorreliert ist (sogenannte Exogenität).^[1] Eine endogene erklärende Variable in einem multiplen Regressionsmodell ist eine erklärende Variable, die entweder aufgrund einer ausgelassenen Variablen, eines Messfehlers oder wegen Simultanität mit der Störgröße korreliert ist (sogenannte Endogenität).^[1]

Verzögerte exogene und endogene Variablen sind in simultanen Gleichungsmodellen exogene oder endogene Variablen, deren Werte um eine oder mehrere Perioden zurückliegen (Verzögerungseffekt).^[3] Die verzögerten exogenen und die verzögerten endogenen Variablen gehören zu den vorherbestimmten Variablen.^[4]

• Strukturgleichungsmodell

1. ↑ ^{a b c} Jeffrey Marc Wooldridge: Introductory econometrics: A modern approach. 5. Auflage. Nelson Education, 2013, S. 848.
2. ↑ N. Gregory Mankiw: Makroökonomik: Mit vielen Fallstudien, 6., überarb. und erg. Auflage, Schäffer-Poeschel Verlag (2011), S. 9 ff.
3. ↑ Jeffrey Marc Wooldridge: Introductory econometrics: A modern approach. 5. Auflage. Nelson Education, 2013, S. 851.
4. ↑ Bernd Rönz und Erhard Förster: Regressions- und Korrelationsanalyse: Grundlagen – Methoden – Beispiele. , S. 258.