#This source code is public domain
#Author: Christian Schirm
import numpy, scipy.spatial
import matplotlib.pyplot as plt
import imageio
def covMat(x1, x2, covFunc, noise=0): # Covariance matrix
cov = covFunc(scipy.spatial.distance_matrix(numpy.atleast_2d(x1).T, numpy.atleast_2d(x2).T))
if noise: cov += numpy.diag(numpy.ones(len(cov))*noise)
return cov
numpy.random.seed(107)
covFunc1 = lambda d: 2*numpy.exp(-numpy.abs(numpy.sin(1.55*numpy.pi*d))**1.9/3 - d**2/7.)
covFunc2 = lambda d: 1*numpy.exp( - d**2/6.)
covFunc = lambda d: 1.5*numpy.exp(-numpy.abs(numpy.sin(1.55*numpy.pi*d))**1.9/3 - d**2/10.)
n=60
x = numpy.linspace(0, 10, 300)
y1 = numpy.random.multivariate_normal(x.ravel()*0, covMat(x, x, covFunc1, noise=0.00))
y2 = numpy.random.multivariate_normal(x.ravel()*0, covMat(x, x, covFunc2, noise=0.00))
x_known = numpy.concatenate([x[:n+1], x[-n:]])
y_known = numpy.concatenate([y1[:n+1], y2[-n:]])
x_unknown = x[n:-n+1]
Ckk = covMat(x_known, x_known, covFunc, noise=0.000001)
Cuu = covMat(x_unknown, x_unknown, covFunc, noise=0.00)
CkkInv = numpy.linalg.inv(Ckk)
Cuk = covMat(x_unknown, x_known, covFunc, noise=0.0)
m = 0 #numpy.mean(y)
covPost = Cuu - numpy.dot(numpy.dot(Cuk,CkkInv),Cuk.T)
y_unknown = numpy.dot(numpy.dot(Cuk,CkkInv),y_known)
fig = plt.figure(figsize=(4.0,2))
sigma = numpy.sqrt(numpy.diag(covPost))
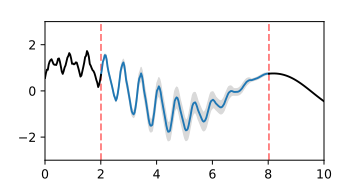
plt.plot(x_unknown, y_unknown, label=u'Prediction')
plt.fill_between(x_unknown.ravel(), y_unknown - sigma, y_unknown + sigma, color = '0.85')
plt.plot(x[:n+1], y1[:n+1],'k-')
plt.plot(x[-n:], y2[-n:],'k-')
plt.vlines([x[n], x[-n]],-3,3,colors='r', linestyles='--', alpha=0.5)
plt.axis([0,10,-3,3])
plt.savefig('Gaussianprocess_gapMean.svg')
fig = plt.figure(figsize=(4.0,2))
for c in 'C1 C4 C2'.split():
y_random = numpy.random.multivariate_normal(x_unknown.ravel()*0, covPost)
plt.plot(x_unknown, y_unknown + y_random, c, label=u'Prediction')
sigma = numpy.sqrt(numpy.diag(covPost))
plt.plot(x[:n+1], y1[:n+1],'k-')
plt.plot(x[-n:], y2[-n:],'k-')
plt.vlines([x[n], x[-n]],-3,3,colors='r', linestyles='--', alpha=0.5)
plt.axis([0,10,-3,3])
plt.savefig('Gaussianprocess_gap.svg')
# Uncertainty animation
numpy.random.seed(1)
t = numpy.arange(0, 1, 0.02)
covFunc = lambda d: numpy.exp(-(3*numpy.sin(d*numpy.pi))**2) # Covariance function
chol = numpy.linalg.cholesky(covMat(t, t, covFunc, noise=1E-5))
r = chol.dot(numpy.random.randn(len(t), len(covPost)))
cov = covPost+1E-5*numpy.identity(len(covPost))
rSmooth = numpy.linalg.cholesky(cov).dot(r.T)
images = []
fig = plt.figure(figsize=(4.0,2))
for ti in [0]+list(range(len(t))):
plt.plot(x_unknown, y_unknown + rSmooth[:,ti], label=u'Prediction',alpha=1)
#plt.fill_between(x_unknown.ravel(), y_unknown - sigma, y_unknown + sigma, color = '0.85')
plt.plot(x[:n+1], y1[:n+1],'k-')
plt.plot(x[-n:], y2[-n:],'k-')
plt.vlines([x[n], x[-n]],-3,3,colors='r', linestyles='--', alpha=0.5)
plt.axis([0,10,-3,3])
plt.xlabel('t')
#plt.tight_layout()
fig.canvas.draw()
s, (width, height) = fig.canvas.print_to_buffer()
images.append(numpy.fromstring(s, numpy.uint8).reshape((height, width, 4)))
fig.clf()
# Save GIF animation
imageio.mimsave('Gaussianprocess_gapUncertainty.gif', images[1:])