Koordinatsystem for himmelrummet
| Sammenskrivningsforslag Artiklen Astronomisk koordinatsystem er foreslået føjet ind i Koordinatsystem for himmelrummet. (Siden oktober 2024) Diskutér forslaget |
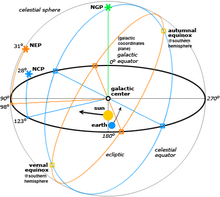
I astronomi er et koordinatsystem for himmelrummet, et sfærisk koordinatsystem, der benyttes til at fastlægge positioner på himmelkuglen. Der findes flere forskellige sådanne koordinatsystemer, som hver angiver nogle koordinater, der er projekteret på himmelkuglen, analogt med de geografiske koordinater, som benyttes til positionsbestemmelse på Jordens overflade. De forskellige koordinatsystemer adskiller sig fra hinanden ved deres forskellige grundplan, som deler himlen i to lige store halvkugler langs en storcirkel. Eksempelvis er grundplanet for det geografiske system Jordens ækvator. Hvert koordinatsystem er derfor navngivet ud fra det grundplan, det er baseret på.
Koordinatsystemer
| Koordinatsystem | Centrum (Origo) | Grundplan | Poler (evt. symbol) | Koordinater (symbol) | Primær retning (0,0) | |
|---|---|---|---|---|---|---|
| i grundplan | mod polerne | |||||
| Horisontale | observatør (topocentrisk) |
horisont | zenith/nadir | azimut (az) | elevation (a) el. højde (h) |
horisontens nord- eller syd-punkt |
| Ækvatoriale | Jordens centrum (geocentrisk) eller Solens centrum (heliocentrisk) |
himlens ækvator samme plan som ækvator |
himmelpoler (NP, SP) |
rektascension (α) eller timevinkel (ha) |
deklination δ | forårspunktet |
| Ekliptiske | ekliptika | ekliptiske poler (ENP, ESP) |
ekliptisk længde (λ) | ekliptisk bredde (β) | ||
| Galaktiske | Solens centrum (heliocentrisk) |
galaktiske plan (mælkevejen) |
galaktiske poler (GNP, GSP) |
galaktisk længde (ℓ) | galaktisk bredde (b) | galaktiske center ved Sgr A* |
| Supergalaktisk | supergalaktiske | supergalaktiske poler (SGNP, SGSP) |
supergalaktisk længde (SGL) |
supergalaktisk bredde (SGB) |
skæringen ml. supergalaktiske- og galaktiske plan | |
Ækvatoriale koordinatsystem
De mest anvendte angivelser af polernes og ækvators beliggenhed sker i forhold til det ældre B1950 eller det moderne J2000-system, men en pol- og ækvatorbeliggenhed på en "aktuel dato" kan også benyttes, dvs. den, som passende svarer til den dato, der er tale om. Dette sidste kan f.eks. være, hvornår en planets eller et rumskibs position er målt. Den "aktuelle dato" kan underinddeles i "gennemsnit for datoen", hvor koordinaterne udligner eller ser bort fra nutation, og "sand dato," som tager nutation i betragtning.
Elevationsvinkel
Elevationsvinklen, der også betegnes som højden, henviser til den lodrette vinkel, som måles fra den geometriske horisont (0°) i retning mod zenith (+90°). Den antager negative værdier for positioner under horisonten, ned til nadir (-90°). Selvom en højde almindeligvis er en lineær længdeenhed, som derfor udtrykkes i metersystemet, udtrykker den i dette system en vinkelafstand.
Udtrykket zenithdistance bruges oftere i astronomien og er komplementærvinkel til højden, så den er 0° i zenith, 90° ved horisonten og 180° ved nadir.
Omregning af koordinater
Fra ækvatoriale til horisontale koordinater
Lad δ være deklinationen og timevinklen.
Lad φ være observatørens breddekreds.
Lad El være elevationsvinklen og Az azimutvinklen.
Lad θ være zenithdistancen.
Så er omregningsligningerne:
Koordinaternes værdi findes ved brug af de inverse trigonometriske funktioner.
Bemærk: Invers cosinus giver dobbelt værdi, så f.eks. 160° og 200° har samme cosinus. Derfor skal resultatet korrigeres, så hvis H < 180 (eller Pi radianer), er Az = 360 – den Az, som ligningerne giver.
Se også
Eksterne henvisninger
- Artiklen baserede oprindelig på Jason Harris' Astroinfo, som følger ed KStars, et pc-planetarium til Linux/KDE. Se http://edu.kde.org/kstars/index.phtml



