Idealgas
 Denne artikel omhandler den klassiske idealgas. For andre idealgasser, se Idealgas (flertydig).
Denne artikel omhandler den klassiske idealgas. For andre idealgasser, se Idealgas (flertydig).

Idealgassen er en idealiseret model, der kan bruges på mange virkelige gasser. En idealgas består af mikroskopiske partikler, jf. den kinetiske gasteori, hvis kinetiske energi udgør gassens indre energi. Flere af de makroskopiske størrelser i idealgassen er relaterede vha. idealgasligningen.[1]
Antagelser og anvendelighed
For den ideale gas antages det, at den består af punktformede partikler, der kan bevæge sig i tre dimensioner. Partiklerne kan støde ind i hinanden ved fuldstændigt elastiske kollisioner, men interagerer ellers ikke, og der er således ikke nogen potentiel energi. Den kinetiske energi beregnes klassisk, så modellen tager ikke højde for relativistiske effekter.[1]
Idealgassen er altså mest præcis som model ved:[2]
- Høje temperaturer: Ved høje temperaturer har gasmolekylerne så høj kinetisk energi , at den potentielle energi , der kommer af interaktionen mellem molekylerne, er meget mindre:
- Lavt tryk: Ved lavt tryk er der så stor afstand mellem molekylerne, at man kan se bort fra molekylernes ekskluderede volumen .
- .
- Ikke-relativistiske hastigheder: Hvis partiklernes hastighed kommer tæt på lysets hastighed , skal der tager højde for relativistisk mekanik, hvilket gøres for relativistiske gasser.[1]
Modellen tager heller ikke højde for faseovergange, da en idealgas ikke kan kondensere og blive til en væske; i så fald skal andre modeller såsom van der Waals-gassen tages i brug.[3]. I en idealgas er kvantemekaniske effekter ligeledes fraværende.[1]
På trods af begrænsningerne er idealgassen dog en simpel og praktisk model, der kan bruges til at forstå varmekraftmaskiner. Den bruges også inden for astrofysik og atmosfæriske fysik[1] såsom i den barometriske højdeformel.[4]
Kinetisk og indre energi
Siden partiklerne i en idealgas ikke interagerer med hinanden, er partiklernes energi blot deres kinetiske energi givet ved:
hvor er en partikels masse, og er hastigheden. Det kan vises, at partiklernes hastighed er Maxwell-Boltzmann-fordelt, og den gennemsnitlige kinetiske energi for en partikel er derfor også givet ved:[5]
hvor er Boltzmanns konstant, og er temperaturen. Energien er altså proportional med temperaturen, hvilket stemmer overens med den brede forståelse af temperatur.
Den samlede energi for hele gassen - dvs. den indre energi - er nu blot den gennemsnitlige kinetiske energi gange antallet af partikler :
Dette kan også udtrykkes vha. stofmængde :
hvor Boltzmanns konstant er erstattet af gaskonstanten .[6]
Idealgasligningen

I en beholder vil sammenstød mellem partikler og beholderens vægge blive målt som et tryk på makroskopisk niveau. Siden temperaturen er relateret til kinetisk energi, kan det vises, at den også er relateret til tryk og volumen ved:
Dette er idealgasligningen.[7] Ligningen blev oprindeligt udledt vha. forsøg på virkelige gasser, hvilket viser idealgassens anvendelighed som model.[1]
Varmekapacitet
Varmekapaciteterne - hvor meget varme, der skal tilføres, for at hæve temperaturen - for konstant volumen og konstant tryk er generelt givet ved:
For en idealgas bliver den første:
Varmekapaciteten er altså proportional med gaskonstanten.
Ved konstant tryk kan det anvendes, at den indre energi ikke kan ændre sig, hvis temperaturen er konstant:
Vha. idealgasligningen kan den afledte til volumenet med hensyn til temperatur ved konstant tryk skrives som:
Varmekapaciteten ved konstant tryk er derfor:
Adiabateksponenten er derfor:
og altså:[6]
Termodynamiske processer
En idealgas kan udsættes for termodynamiske processer og kan derfor bruges til at modellere varmekraftmaskiner.[8]
Isoterm proces

For en isoterm proces er temperaturen konstant, hvilket gør hele højresiden i idealgasligningen til en konstant:
For en isoterm kompression er tryk og volumen altså omvendt proportionale:
Da den indre energi kun afhænger af temperatur, ændrer den sig ikke
og den tilførte varme udlignes derfor af arbejdet
Arbejdet er givet ved
Trykket er omvendt proportionalt med volumenet, så integralet er:
Varmen er dermed:
Det ses, at gassen modtager varme under en ekspansion, men mister varme under en kompression.[9]
Isobar proces

For en isobar proces er trykket konstant, hvilket betyder, at volumen og temperatur er proportionale:
Arbejdet er
mens ændringen indre energi er
Varmen er tilsvarende:
Pga. varmetab mister gassen altså energi, når den pressen sammen. Dette gør den for at undgå, at trykket stiger. Vha. udtrykket for indre energi, kan dette også skrives som
Det ses, at faktoren foran temperaturændringen er , hvilket var forventeligt.
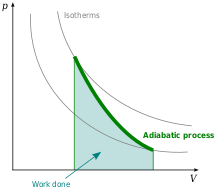
Adiabatisk proces
Under en adiabatisk proces bliver der ikke overført nogen varme:
Differentialet for den indre energi er derfor blot:
Men differentialet kan også skrives som:
Disse to udtryk sætter lig hinanden, og trykket erstattes vha. idealgasligningen:
De variable separeres, og faktorer flyttes til venstre side:
Begge sider integreres:
Det ses, at eksponenten er relateret til adiabateksponentet ved:
Så for en adiabatisk proces gælder bevarelsesloven:
Med idealgasligningen kan temperatur også erstattes med tryk:
Der gælder altså tilsvarende for tryk og volumen:
eller
Adiabateksponenten er større end 1, så i et pV-diagram er kurven for en adiabatisk proces stejlere end for en isoterm proces.[10]
Isometrisk proces

For en isometrisk proces er volumenet konstant, hvilket betyder, at tryk og temperatur er proportionale:
Hvis en lukket beholder opvarmes, vil trykket i den altså stige.
Der kan ikke udføres volumenarbejde:
så varmeoverførslen er lig med ændringen i indre energi
Ved at indsætte den indre energi er varmen relateret til temperaturændringen ved:
Det ses, at faktoren er lig med som forventet. Vha. idealgasligningen kan varmen alternativ udtrykkes som:
Kildehenvisninger
- ^ a b c d e f Blundell, Stephen J.; Blundell, Katherine M. (2006). "1.3 The ideal gas". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 6-7. ISBN 978-0-19-856770-7.
- ^ Cengel, Yunus A.; Boles, Michael A. Thermodynamics: An Engineering Approach (4th udgave). s. 89. ISBN 0-07-238332-1.
- ^ Blundell, Stephen J.; Blundell, Katherine M. (2006). "26.1 The van der Waals gas". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 280-288. ISBN 978-0-19-856770-7.
- ^ Blundell, Stephen J.; Blundell, Katherine M. (2006). "4.7 Applications of the Boltzmann distribution". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 41-42. ISBN 978-0-19-856770-7.
- ^ Blundell, Stephen J.; Blundell, Katherine M. (2006). "5.2 The speed distribution". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 47-48. ISBN 978-0-19-856770-7.
- ^ a b Blundell, Stephen J.; Blundell, Katherine M. (2006). "11.3 Heat capacity". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 109-110. ISBN 978-0-19-856770-7.
- ^ Blundell, Stephen J.; Blundell, Katherine M. (2006). "6.2 The ideal gas law". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 56-57. ISBN 978-0-19-856770-7.
- ^ Blundell, Stephen J.; Blundell, Katherine M. (2006). "13.2 The Carnot engine". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 123-125. ISBN 978-0-19-856770-7.
- ^ Blundell, Stephen J.; Blundell, Katherine M. (2006). "12.2 Isothermal expansion of an ideal gas". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 116. ISBN 978-0-19-856770-7.
- ^ Blundell, Stephen J.; Blundell, Katherine M. (2006). "12.3 Adiabatic expansion of an ideal gas". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 117. ISBN 978-0-19-856770-7.


























![{\displaystyle {\begin{aligned}C_{V}&=\left({\frac {\partial U}{\partial T}}\right)_{V}\\C_{p}&=C_{V}+\left[\left({\frac {\partial U}{\partial V}}\right)_{T}+p\right]\left({\frac {\partial V}{\partial T}}\right)_{p}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1055f82406d28bac85d43b912865578260323189)



![{\displaystyle {\begin{aligned}C_{p}&=C_{V}+\left[0+p\right]{\frac {nR}{p}}\\C_{p}&={\frac {3}{2}}nR+nR\\C_{p}&={\frac {5}{2}}nR\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb4292dbe381285a32f0172ad184d69e51d7770d)





























